题目内容
1.已知函数f(x)=$\left\{\begin{array}{l}{{3}^{-x},}&{x≤0}\\{\sqrt{x},}&{x>0}\end{array}\right.$,若函数g(x)=f(x)-x-k有且仅有两个零点,则实数k的取值范围是(0,$\frac{1}{4}$).分析 由题意可转化为函数f(x)=与函数y=x+k的图象有且仅有两个交点,从而作图求解即可.
解答 解:函数g(x)=f(x)-x-k有且仅有两个零点,
∴y=f(x)与y=x+k的图象的图象有且仅有两个交点,
分别画出y=f(x)与y=x+k的图象的图象,如图所示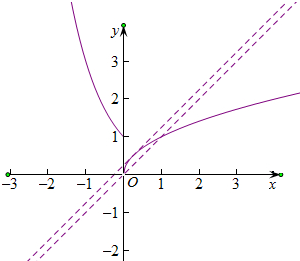
当b=0时,有一个交点,是一个临界值,
当直线y=x+k与f(x)=$\sqrt{x}$相切时,
∴f′(x)=$\frac{1}{2}{x}^{-\frac{1}{2}}$=1;
∴x=$\frac{1}{4}$,
∴f($\frac{1}{4}$)=$\frac{1}{2}$,
故切点为($\frac{1}{4}$,$\frac{1}{2}$);
故b=$\frac{1}{2}$-$\frac{1}{4}$=$\frac{1}{4}$;
结合图象可得,k∈(0,$\frac{1}{4}$)
故答案为:(0,$\frac{1}{4}$).
点评 本题考查了导数的应用,函数图象的作法及函数的零点与函数的图象的交点的关系应用等,同时考查了数形结合的思想应用,属于中档题

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
10.下列函数中,既是偶函数又在(0,+∞)上单调递增的是( )
| A. | y=ex | B. | y=cosx | C. | y=|x|+1 | D. | y=$\sqrt{x}$ |