题目内容
(本题满分16分)已知二次函数f (x) = x2 ??ax + a (x∈R)同时满足:①不等式 f (x) ≤ 0的解集有且只有一个元素;②在定义域内存在0 < x1 < x2,使得不等式f (x1) > f (x2)成立.设数列{an}的前 n 项和Sn = f (n).(1)求函数f (x)的表达式;(2)求数列{an}的通项公式;(3)在各项均不为零的数列{cn}中,若ci·ci+1 < 0,则称ci,ci+1为这个数列{cn}一对变号项.令cn = 1 ?? (n为正整数),求数列{cn}的变号项的对数.
(Ⅰ) a = 4, f (x) = x2 ??4x + 4. (Ⅱ) an = (Ⅲ)共有3对变号项
解析:
(1)∵f (x) ≤ 0的解集有且只有一个元素,
∴ △ = a2 ??4a = 0 ?? a = 0或a = 4, 1分
当 a = 4 时,函数f (x) = x2 ??4x + 4在(0,2)上递减,
故存在0 < x1 < x2,使得不等式f (x1) > f (x2)成立. 3分
当 a = 0 时,函数f (x) = x2 在(0,+∞)上递增,
故不存在0 < x1 < x2,使得不等式f (x1) > f (x2)成立.
综上:a = 4, f (x) = x2 ??4x + 4. 5分
⑵由⑴可知:Sn = n2 ??4n + 4. 当 n = 1时,a1 = S1 = 1, 6分
当n ≥ 2时,an = Sn ?? Sn??1= (n2 ??4n + 4) ?? [(n ??1)2 ??4(n ??1) + 4] = 2n ?? 5,
∴ an = 10分
⑶法一:由题设cn = , 12分
∵ 当n ≥ 2时,cn + 1 ?? cn = ?? = ,
∴ 当n ≥ 3时,数列{cn}递增, ∵ c3 = ??3 < 0,又由cn = 1 ?? ≥ 0,得 n ≥ 5,
可知 c4·c5 < 0, 即 n ≥ 3时,有且只有一对变号项, 14分
又 ∵ c1 = ??3,c2 = 5,c3 = ??3,即 c1·c2 < 0,c2·c3 < 0,∴ 此处有2对变号项.
综上可得:数列{cn}的变号项有3对. 16分
法二:当i ≥ 2时,ci = 1 ?? = , ∵ ci·ci+1 < 0 ,
∴ · < 0,∴ < i < 或 < i < , ∵ i ≥ 2,i∈N*,∴ i = 2或4,即 c2·c3 < 0,c4·c5 < 0,此处有2对变号项, 14分又 ∵ c1 = ??3,c2 = 5,即 c1·c2 < 0,此处有一对变号项,综上可得:数列{cn}的共有3对变号项 16分

 ,且对任意
,且对任意 ,有
,有 .
. ;
; 在区间(0,1)上为单调函数,求实
在区间(0,1)上为单调函数,求实 数
数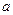 的取值范围.
的取值范围. 的零点个数?(提示
的零点个数?(提示 )
) 为实常数).
为实常数). 时,求函数
时,求函数 在
在 上的最小值;
上的最小值; 在区间
在区间 上有解,求实数
上有解,求实数 的取值范围;
的取值范围;
 )
) :
: 的离心率为
的离心率为 ,
, 分别为椭圆
分别为椭圆 为椭圆上任意一点,以
为椭圆上任意一点,以 为半径作圆
为半径作圆 有公共点时,求△
有公共点时,求△ 面积的最大值.
面积的最大值. 是定义在
是定义在 上的偶函数,且当
上的偶函数,且当 时,
时, 。
。 及
及 的值;
的值; 上的解析式;
上的解析式; 的方程
的方程 有四个不同的实数解,求实数
有四个不同的实数解,求实数 的取值范围。
的取值范围。