题目内容
如图,在平面直角坐标系 中,已知
中,已知 ,
, ,
, 是椭圆
是椭圆 上不同的三点,
上不同的三点, ,
, ,
, 在第三象限,线段
在第三象限,线段 的中点在直线
的中点在直线 上.
上.
(1)求椭圆的标准方程;
(2)求点C的坐标;
(3)设动点 在椭圆上(异于点
在椭圆上(异于点 ,
, ,
, )且直线PB,PC分别交直线OA于
)且直线PB,PC分别交直线OA于 ,
, 两点,证明
两点,证明 为定值并求出该定值.
为定值并求出该定值.
(1)求椭圆方程一般用待定系数法.本题已知椭圆过两点,列两个方程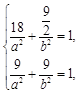 ,解出
,解出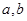 的值,(2)求点
的值,(2)求点 的坐标,需列出两个方程.一是点C在椭圆上,即
的坐标,需列出两个方程.一是点C在椭圆上,即 ,二是
,二是 的中点在直线
的中点在直线 上,即
上,即 .注意到
.注意到 在第三象限,舍去正值.(3)题意明确,思路简洁,就是求出点
在第三象限,舍去正值.(3)题意明确,思路简洁,就是求出点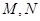 的坐标,算出
的坐标,算出 为定值.难点是如何消去参数.因为点
为定值.难点是如何消去参数.因为点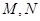 在直线
在直线 :
:  上,所以可设
上,所以可设 ,
, .选择
.选择 作为参数,即用
作为参数,即用 表示点
表示点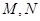 的坐标.由
的坐标.由 三点共线,解得
三点共线,解得 ,同理解得
,同理解得 .从而有
.从而有 ,这里主要用到
,这里主要用到 代入化简.本题也可利用椭圆参数方程或三角表示揭示
代入化简.本题也可利用椭圆参数方程或三角表示揭示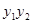 为定值.
为定值.
解析试题分析:(1) ,(2)
,(2) ,(3)
,(3) .
.
试题解析:(1)由已知,得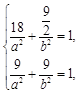 解得
解得 2分
2分
所以椭圆的标准方程为 . 3分
. 3分
(2)设点
 ,则
,则 中点为
中点为 .
.
由已知,求得直线 的方程为
的方程为 ,从而
,从而 .①
.①
又∵点 在椭圆上,∴
在椭圆上,∴ .②
.②
由①②,解得 (舍),
(舍), ,从而
,从而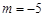 . 5分
. 5分
所以点 的坐标为
的坐标为 . 6分
. 6分
(3)设 ,
, ,
, .
.
∵ 三点共线,∴
三点共线,∴ ,整理,得
,整理,得 . 8分
. 8分
∵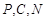 三点共线,∴
三点共线,∴ ,整理,得
,整理,得 . 10分
. 10分
∵点 在椭圆上,∴
在椭圆上,∴ ,
, .
.
从而 . 14分
. 14分
所以 15分
15分
∴ 为定值,定值为
为定值,定值为 . 16分
. 16分
考点:椭圆标准方程,直线与椭圆位置关系

练习册系列答案
相关题目
 的左右焦点分别为
的左右焦点分别为 、
、 ,短轴两个端点为
,短轴两个端点为 、
、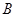 ,且四边形
,且四边形 是边长为2的正方形.
是边长为2的正方形. 分别是椭圆长轴的左右端点,动点
分别是椭圆长轴的左右端点,动点 满足
满足 ,连接
,连接 ,交椭圆于点
,交椭圆于点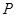 ,证明:
,证明: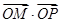 为定值;
为定值; 轴上是否存在异于点
轴上是否存在异于点 的定点
的定点 ,使得以
,使得以 为直径的圆恒过直线
为直径的圆恒过直线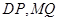 的交点?若存在,求出点Q的坐标;若不存在,请说明理由.
的交点?若存在,求出点Q的坐标;若不存在,请说明理由. :
: ,命题
,命题 :方程
:方程 表示焦点在
表示焦点在 轴上的双曲线.
轴上的双曲线. 的取值范围;
的取值范围; ”为真,命题“
”为真,命题“ ”为假,求实数
”为假,求实数 的焦点在
的焦点在 轴上,离心率为
轴上,离心率为 ,对称轴为坐标轴,且经过点
,对称轴为坐标轴,且经过点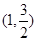 .
. 的方程;
的方程; 与椭圆
与椭圆 相交于
相交于 、
、 两点,
两点,  为原点,在
为原点,在 、
、 点的点
点的点 、
、 ,使得
,使得 在以
在以 为直径的圆外,求直线斜率
为直径的圆外,求直线斜率 的取值范围.
的取值范围. =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ,一条准线方程为x=
,一条准线方程为x=
 ,其左焦点到点P(2,1)的距离为
,其左焦点到点P(2,1)的距离为 .不过原点O的直线l与C相交于A,B两点,且线段AB被直线OP平分.
.不过原点O的直线l与C相交于A,B两点,且线段AB被直线OP平分.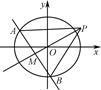
 +y2=1(a>1)的上顶点为M(0,1),两条过M的动弦MA、MB满足MA⊥MB.
+y2=1(a>1)的上顶点为M(0,1),两条过M的动弦MA、MB满足MA⊥MB. ,求a;
,求a;
 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,且过点A(0,1).
,且过点A(0,1).
 .
.