题目内容
若直线3x+4y-3=0与直线6x+my+14=0平行,则它们之间的距离为 .
2
【解析】由两直线平行的条件得3m=4×6,解得m=8,
此时直线6x+my+14=0的方程可化为3x+4y+7=0,∴两直线3x+4y-3=0和3x+4y+7=0间的距离为d=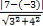
=2.
【误区警示】本题求解时易不将6x+8y+14=0化简,直接求两平行线间的距离,得到d=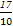
或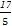
的错误,根本原因是没能掌握好两平行线间距离公式的应用条件.
练习册系列答案
相关题目
题目内容
若直线3x+4y-3=0与直线6x+my+14=0平行,则它们之间的距离为 .
2
【解析】由两直线平行的条件得3m=4×6,解得m=8,
此时直线6x+my+14=0的方程可化为3x+4y+7=0,∴两直线3x+4y-3=0和3x+4y+7=0间的距离为d=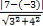=2.
【误区警示】本题求解时易不将6x+8y+14=0化简,直接求两平行线间的距离,得到d=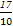或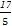的错误,根本原因是没能掌握好两平行线间距离公式的应用条件.
