题目内容
6.已知点(1,$\frac{1}{3}$)是函数f(x)=ax(a>0且a≠1)的图象上一点,等比数列{an}的前n项和为f(n)-c,数列{bn}(bn>0)的首项为c,且前n项和Sn满足Sn-Sn-1=$\sqrt{{S}_{n}}$+$\sqrt{{S}_{n-1}}$(n≥2).(1)求数列{an}和{bn}的通项公式;
(2)若数列{$\frac{1}{{b}_{n}{b}_{n+1}}$}前n项和为Tn,则满足Tn>$\frac{1000}{2015}$的最小正整数n是多少?
分析 (1)由f(1)=a=$\frac{1}{3}$,解得a=$\frac{1}{3}$,可得f(x)=$(\frac{1}{3})^{x}$.a1=f(1)-c=$\frac{1}{3}$-c,当n≥2时,an=[f(n)-c]-[f(n-1)-c],可得a2,a3,利用等比数列的性质可得:${a}_{2}^{2}={a}_{1}•{a}_{3}$,解得c=1.可得an.由于Sn-Sn-1=$(\sqrt{{S}_{n}}+\sqrt{{S}_{n-1}})$$(\sqrt{{S}_{n}}-\sqrt{{S}_{n-1}})$=$\sqrt{{S}_{n}}$+$\sqrt{{S}_{n-1}}$(n≥2),可得$\sqrt{{S}_{n}}$-$\sqrt{{S}_{n-1}}$=1,利用等差数列的通项公式可得:Sn,利用递推公式可得bn.
(2)$\frac{1}{{b}_{n}{b}_{n+1}}$=$\frac{1}{2}(\frac{1}{2n-1}-\frac{1}{2n+1})$,利用“裂项求和”可得Tn,即可得出.
解答 解:(1)∵f(1)=a=$\frac{1}{3}$,解得a=$\frac{1}{3}$,
∴f(x)=$(\frac{1}{3})^{x}$.
a1=f(1)-c=$\frac{1}{3}$-c,
a2=[f(2)-c]-[f(1)-c]=-$\frac{2}{9}$,
a3=[f(3)-c]-[f(2)-c]=-$\frac{2}{27}$,
又数列{an}成等比数列,
∴${a}_{2}^{2}={a}_{1}•{a}_{3}$,
∴$(-\frac{2}{9})^{2}$=-$\frac{2}{27}$×$(\frac{1}{3}-c)$,
解得c=1.
又公比$q=\frac{{a}_{2}}{{a}_{1}}$=$\frac{1}{3}$,
∴an=-$\frac{2}{3}×(\frac{1}{3})^{n-1}$=-2×$(\frac{1}{3})^{n}$(n∈N*).
∵Sn-Sn-1=$(\sqrt{{S}_{n}}+\sqrt{{S}_{n-1}})$$(\sqrt{{S}_{n}}-\sqrt{{S}_{n-1}})$=$\sqrt{{S}_{n}}$+$\sqrt{{S}_{n-1}}$(n≥2).
又bn>0,$\sqrt{{S}_{n}}$>0,
∴$\sqrt{{S}_{n}}$-$\sqrt{{S}_{n-1}}$=1.,
∴数列$\{\sqrt{{S}_{n}}\}$构成一个首项为1公差为1的等差数列,
∴$\sqrt{{S}_{n}}$=1+(n-1)×1=n,
∴Sn=n2,
当n=1,b1=S1=1,
当n≥2时,bn=Sn-Sn-1=n2-(n-1)2=2n-1,
当n=1时,上式也成立.
∴bn=2n=1(n∈N*).
(2)$\frac{1}{{b}_{n}{b}_{n+1}}$=$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}(\frac{1}{2n-1}-\frac{1}{2n+1})$,
∴Tn=$\frac{1}{2}[(1-\frac{1}{3})+(\frac{1}{3}-\frac{1}{5})$+…+$(\frac{1}{2n-1}-\frac{1}{2n+1})]$
=$\frac{1}{2}(1-\frac{1}{2n+1})$
=$\frac{n}{2n+1}$.
由Tn=$\frac{n}{2n+1}$>$\frac{1000}{2015}$,可得$n>\frac{200}{3}$=66+$\frac{2}{3}$,
因此满足Tn>$\frac{1000}{2015}$的最小正整数为67.
点评 本题考查了递推关系、“裂项求和”方法、等差数列与等比数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案| A. | p或q | B. | p且q | C. | p或q | D. | p且q |
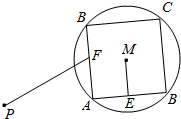 如图,已知圆M的半径为2,点P与圆心M的距离为4,正方形ABCD是圆M的内接四边形,E,F是边AB,AD的中点,当正方形ABCD绕圆心M转动时,$\overrightarrow{PF}$•$\overrightarrow{ME}$的取值范围是( )
如图,已知圆M的半径为2,点P与圆心M的距离为4,正方形ABCD是圆M的内接四边形,E,F是边AB,AD的中点,当正方形ABCD绕圆心M转动时,$\overrightarrow{PF}$•$\overrightarrow{ME}$的取值范围是( )| A. | [-2,2] | B. | [-2$\sqrt{2}$,2$\sqrt{2}$] | C. | [-4,4] | D. | [-4$\sqrt{2}$,4$\sqrt{2}$] |
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | 1 | D. | 2 |
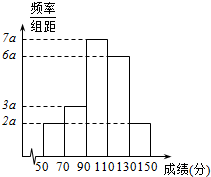 贵阳市某数学教师从他所教的2015届高三(X)班与高三(Y)班学生的高考数学成绩中,随机抽取20名学生的成绩绘制成频率分布直方图,如图所示.
贵阳市某数学教师从他所教的2015届高三(X)班与高三(Y)班学生的高考数学成绩中,随机抽取20名学生的成绩绘制成频率分布直方图,如图所示.