题目内容
【题目】已知直线
:
,（t为参数）,曲线
:
,(
为参数).
（1）以原点为极点,x轴正半轴为极轴建立极坐标系；当
时,求与的交点的极坐标（其中极径
,极角
）；
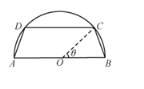
（2）过坐标原点O作的垂线,垂足为A,P为OA中点,当
变化时,求P点轨迹的参数方程,并指出它是什么曲线.
【答案】（1）
,
（2）
,轨迹是圆心为
,半径为
的圆
【解析】
（1）先把极坐标方程化成普通方程，求出交点坐标后，再化成极坐标，即可得答案；
（2）先将
参数方程化为普通方程，写出A点坐标为
，利用中点坐标公式得到
的坐标，消参后即可得答案.
（1）当
时,的普通方程为
,
的普通方程为
，
联立方程组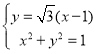
,解得与的交点坐标为
,
．
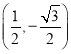所以两点的极坐标为,
.
（2）的普通方程为
,设A点坐标为,
故当
变化时,P点轨迹的参数方程为
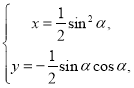（为参数）
P点轨迹的普通方程为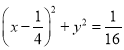
．
故P点轨迹是圆心为
,半径为的圆．
练习册系列答案
相关题目
