题目内容
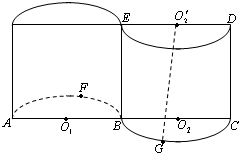 如图所示的几何体,是将高为2、底面半径为1的圆柱沿过旋转轴的平面切开后,将其中一半沿切面向右水平平移后形成的封闭体.
如图所示的几何体,是将高为2、底面半径为1的圆柱沿过旋转轴的平面切开后,将其中一半沿切面向右水平平移后形成的封闭体. 分别为AB,BC,DE的中点,F为弧AB的中点,G为弧BC的中点.
分别为AB,BC,DE的中点,F为弧AB的中点,G为弧BC的中点.
(1)求这个几何体的表面积;
(2)求异面直线AF与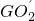 所成的角的大小(结果用反三角函数值表示).
所成的角的大小(结果用反三角函数值表示).
解:(1)将圆柱按题中方法切开,再平移后接成封闭体后,该几何体的表面积比原来的圆柱表面积多了两个轴截面矩形的面积,
因此它的表面积为S表=S圆柱表+2SBCDE=(2π×12+2π×1×2)+2×2×2=6π+8; …(6分)
(2)连接AF、CG、CO2',则AF∥CG,
所以∠CGO2'或其补角为异面直线AF与GO2'所成的角.…(9分)
在△CGO2'中,GO2'=CO2'= =
= ,CG=
,CG= =
= ,…(12分)
,…(12分)
∵cos∠CGO2'=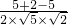 =
= ,
,
∴∠CGO2'=arccos ,即异面直线AF与GO2'所成的角的大小为arccos
,即异面直线AF与GO2'所成的角的大小为arccos .…(14分)
.…(14分)
分析:(1)由题意,变化后形成的封闭体表面比原来的圆柱表面多了两个轴截面的面积,由此不难结合已知数据计算出它的表面积.
(2)连接AF、CG、CO2',则可得∠CGO2'或其补角为异面直线AF与GO2'所成的角.然后在△CGO2'中,计算出各边的长,利用余弦定理即可求出异面直线AF与GO2'所成的角的余弦值,从而得出异面直线AF与GO2'所成的角大小.
点评:本题将一个圆柱体一分为二,求平移后的表面积和异面直线所成角的大小,着重考查了旋转体表面积的求法和异面直线所成角等知识,属于基础题.

因此它的表面积为S表=S圆柱表+2SBCDE=(2π×12+2π×1×2)+2×2×2=6π+8; …(6分)
(2)连接AF、CG、CO2',则AF∥CG,
所以∠CGO2'或其补角为异面直线AF与GO2'所成的角.…(9分)
在△CGO2'中,GO2'=CO2'=
 =
= ,CG=
,CG= =
= ,…(12分)
,…(12分)∵cos∠CGO2'=
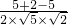 =
= ,
,∴∠CGO2'=arccos
 ,即异面直线AF与GO2'所成的角的大小为arccos
,即异面直线AF与GO2'所成的角的大小为arccos .…(14分)
.…(14分)分析:(1)由题意,变化后形成的封闭体表面比原来的圆柱表面多了两个轴截面的面积,由此不难结合已知数据计算出它的表面积.
(2)连接AF、CG、CO2',则可得∠CGO2'或其补角为异面直线AF与GO2'所成的角.然后在△CGO2'中,计算出各边的长,利用余弦定理即可求出异面直线AF与GO2'所成的角的余弦值,从而得出异面直线AF与GO2'所成的角大小.
点评:本题将一个圆柱体一分为二,求平移后的表面积和异面直线所成角的大小,着重考查了旋转体表面积的求法和异面直线所成角等知识,属于基础题.

练习册系列答案
相关题目
 (2012•浦东新区一模)如图所示的几何体,是将高为2、底面半径为1的圆柱沿过旋转轴的平面切开后,将其中一半沿切面向右水平平移后形成的封闭体.
(2012•浦东新区一模)如图所示的几何体,是将高为2、底面半径为1的圆柱沿过旋转轴的平面切开后,将其中一半沿切面向右水平平移后形成的封闭体. (2012•黄浦区二模)如图所示的几何体,是由棱长为2的正方体ABCD-A1B1C1D1截去一个角后所得的几何体.
(2012•黄浦区二模)如图所示的几何体,是由棱长为2的正方体ABCD-A1B1C1D1截去一个角后所得的几何体. 是边长为2的正三角形. 若
是边长为2的正三角形. 若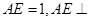 平面
平面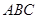 ,平面
,平面 平面
平面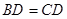 ,且
,且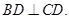
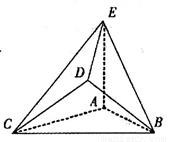
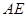 //平面
//平面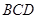 ;
; 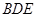
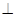 平面
平面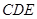 .
. 
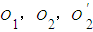 分别为AB,BC,DE的中点,F为弧AB的中点,G为弧BC的中点.
分别为AB,BC,DE的中点,F为弧AB的中点,G为弧BC的中点.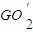 所成的角的大小(结果用反三角函数值表示).
所成的角的大小(结果用反三角函数值表示).