题目内容
【题目】设圆x2+y2=12与抛物线x2=4y相交于A,B两点,F为抛物线的焦点,若过点F且斜率为1的直线l与抛物线和圆交于四个不同的点,从左至右依次为P1 , P2 , P3 , P4 , 则|P1P2|+|P3P4|的值 , 若直线m与抛物线相交于M,N两点,且与圆相切,切点D在劣弧 ![]() 上,则|MF|+|NF|的取值范围是 .
上,则|MF|+|NF|的取值范围是 .
【答案】5 ![]() ;[2+4
;[2+4 ![]() ,22]
,22]
【解析】解:由 ![]() ,得
,得 ![]() 或
或 ![]() ,
,
即A(﹣2 ![]() ,2),B(2
,2),B(2 ![]() ,2).
,2).
∵点F坐标为(0,1),∴kFB= ![]() ,∴kl>kFB ,
,∴kl>kFB ,
所以直线l与圆交于P1、P3两点,与抛物线交于P2、P4两点,
设P1(x1 , y1),P2(x2 , y2),P3(x3 , y3),P4(x4 , y4)
把直线l方程:y=x+1代入x2=4y,得x2﹣4x﹣4=0,∴x2+x4=4;
把直线l方程:y=x+1代入x2+y2=12,得2x2+2x﹣11=0,∴x1+x3=﹣1
∴|P1P2|+|P3P4|= ![]() [(x2﹣x1)+(x4﹣x3)]=
[(x2﹣x1)+(x4﹣x3)]= ![]() [(x2+x4)﹣(x1+x3)]=5
[(x2+x4)﹣(x1+x3)]=5 ![]()
所以|P1P2|+|P3P4|的值等于5 ![]() .
.
设直线m的方程为y=k+b(b>0),
代入抛物线方程得x2﹣4kx﹣4b=0,
设点M(x1 , y1),N(x2 , y2),则x1+x2=4k,
则y1+y2=k(x1+x2)+2b=4k2+2b,
∵直线m与该圆相切,∴ ![]() =
= ![]() ,即
,即 ![]() ,
,
又|MF|=y1+1,|NF|=y2+1,
∴|MF|+|NF|=y1+y2+2=4k2+2b+2= ![]()
∵kOA=﹣ ![]() ,kOB=
,kOB= ![]() ,∴分别过A、B的圆的切线的斜率为
,∴分别过A、B的圆的切线的斜率为 ![]() ,﹣
,﹣ ![]() .
.
∴k∈[﹣ ![]() ,
, ![]() ],∴0≤k2≤2,∴0≤
],∴0≤k2≤2,∴0≤ ![]() ﹣1≤12,
﹣1≤12,
∵b>0,∴b∈[2 ![]() ,6]
,6]
所以|MF|+|NF|的取值范围为[2+4 ![]() ,22].
,22].
故答案为:5 ![]() ;[2+4
;[2+4 ![]() ,22].
,22].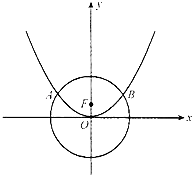
由圆的方程和抛物线的方程联解,求得交点A、B的坐标,从而判断直线l与圆交于P1、P3 , 直线l与抛物线交于P2、P4 , 另|P1P2|+|P3+P4|的表达式用P1 , P2 , P3 , P4的四点的横坐标表示,然后根据根与系数的关系,代入表达式,即解;先设直线m的方程y=k+b,交点M、N坐标,再用点M、N纵坐标表示出|MF|+|NF|,由与圆相切,得到k与b的关系,消去k用b表示|MF|+|NF|,即得到关于b的一个函数,由kOA=﹣ ![]() ,kOB=
,kOB= ![]() ,得到k的范围,由此求得b的范围,再将b的代入|MF|+|NF|的函数关系式中并求出其范围.
,得到k的范围,由此求得b的范围,再将b的代入|MF|+|NF|的函数关系式中并求出其范围.
