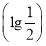Question

已知函数f(x)＝x2＋xsin x＋cos x.

(1)若曲线y＝f(x)在点(a，f(a))处与直线y＝b相切，求a与b的值；

(2)若曲线y＝f(x)与直线y＝b有两个不同交点，求b的取值范围．

 

Answer 1

(1) a＝0，b＝1.(2) b>1

【解析】(1)由f(x)＝x2＋xsin x＋cos x，

得f′(x)＝x(2＋cos x)，

∵y＝f(x)在点(a，f(a))处与直线y＝b相切．

∴f′(a)＝a(2＋cos a)＝0且b＝f(a)，

则a＝0，b＝f(0)＝1.

(2)令f′(x)＝0，得x＝0.

∴当x>0时，f′(x)>0，f(x)在(0，＋∞)递增．

当x<0时，f′(x)<0，f(x)在(－∞，0)上递减．

∴f(x)的最小值为f(0)＝1.

由于函数f(x)在区间(－∞，0)和(0，＋∞)上均单调，

所以当b>1时曲线y＝f(x)与直线y＝b有且仅有两个不同交点．