题目内容
已知集合A={x|x2-2x-3≤0}，B={x|x2+px+q＜0}，满足A∩B={x|-1≤x＜2}，则p与q的关系为（ ）A．p-q=0
B．p+q=0
C．p+q=-5
D．2p+q=-4
【答案】分析：求出集合A的解集，设B={x|x1＜x＜x2}，根据交集的定义A∩B={x|-1≤x＜2}并观察数轴得x1＜-1，x2=2，所以x=2是方程的解，代入求出即可．
解答：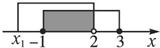
解：化简得：A={x|-1≤x≤3}，
∵A∩B非空，∴B非空，设B={x|x1＜x＜x2}，观察数轴，
有x1＜-1，x2=2，即x=2是方程x2+px+q=0的一根，把x2=2代入x2+px+q=0，有4+2p+q=0．
故选D．
点评：考查学生理解交集为既属于A又属于B的元素，利用数形结合的数学思想解决数学问题．
解答：
解：化简得：A={x|-1≤x≤3}，∵A∩B非空，∴B非空，设B={x|x1＜x＜x2}，观察数轴，
有x1＜-1，x2=2，即x=2是方程x2+px+q=0的一根，把x2=2代入x2+px+q=0，有4+2p+q=0．
故选D．
点评：考查学生理解交集为既属于A又属于B的元素，利用数形结合的数学思想解决数学问题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目