题目内容
【题目】设数列{an}的前n项和为Sn , 已知S2=4,an+1=2Sn+1,n∈N* .
(1)求通项公式an;
(2)求数列{|an﹣n﹣2|}的前n项和.
【答案】
(1)
解:∵S2=4,an+1=2Sn+1,n∈N*.
∴a1+a2=4,a2=2S1+1=2a1+1,
解得a1=1,a2=3,
当n≥2时,an+1=2Sn+1,an=2Sn﹣1+1,
两式相减得an+1﹣an=2(Sn﹣Sn﹣1)=2an,
即an+1=3an,当n=1时,a1=1,a2=3,
满足an+1=3an,
∴ ![]() =3,则数列{an}是公比q=3的等比数列,
=3,则数列{an}是公比q=3的等比数列,
则通项公式an=3n﹣1
(2)
解:an﹣n﹣2=3n﹣1﹣n﹣2,
设bn=|an﹣n﹣2|=|3n﹣1﹣n﹣2|,
则b1=|30﹣1﹣2|=2,b2=|3﹣2﹣2|=1,
当n≥3时,3n﹣1﹣n﹣2>0,
则bn=|an﹣n﹣2|=3n﹣1﹣n﹣2,
此时数列{|an﹣n﹣2|}的前n项和Tn=3+ ![]() ﹣
﹣ ![]() =
= ![]() ,
,
则Tn= 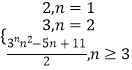 .
.
【解析】(1)根据条件建立方程组关系,求出首项,利用数列的递推关系证明数列{an}是公比q=3的等比数列,即可求通项公式an;(2)讨论n的取值,利用分组法将数列转化为等比数列和等差数列即可求数列{|an﹣n﹣2|}的前n项和.本题主要考查递推数列的应用以及数列求和的计算,根据条件建立方程组以及利用方程组法证明列{an}是等比数列是解决本题的关键.求出过程中使用了转化法和分组法进行数列求和.
【考点精析】认真审题,首先需要了解数列的通项公式(如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式).

【题目】某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
单价x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
(1)求回归直线方程![]() =bx+a;(其中
=bx+a;(其中 ,
,![]() ,
,![]() ,
,![]() ,
,![]() );
);
(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入-成本)