题目内容
1.证明函数f(x)=$\frac{3-x}{x-1}$在(1,+∞)上是减函数.分析 通过函数单调性的定义证明即可.
解答 解:f(x)=$\frac{3-x}{x-1}$=-1+$\frac{2}{x-1}$,x∈(1,+∞),
设x1>x2>1,
则f(x1)-f(x2)=-1+$\frac{2}{{x}_{1}-1}$+1-$\frac{2}{{x}_{2}-1}$=$\frac{2{(x}_{2}{-x}_{1})}{{(x}_{1}-1){(x}_{2}-1)}$,
∵x1>x2>1,x1>x2,x1-1>0,x2>-1>0,
∴f(x1)<f(x2),
∴函数f(x)=$\frac{3-x}{x-1}$在(1,+∞)上是减函数.
点评 本题考查了函数的单调性的证明,是一道基础题.

练习册系列答案
相关题目
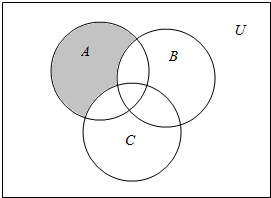
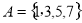 ,
,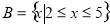 ,则
,则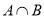 等于
等于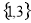 B.
B. 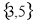 C.
C.  D.
D.