题目内容
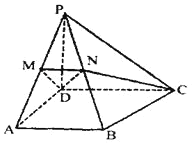
【题目】在四棱锥
中，
，
底面
，
，直线
与底面所成的角为
，
分别是
的中点．
（1）求证：直线
平面
；
（2）若
，求证：直线
平面
；
（3）若
，求棱锥
的体积．
【答案】（1）详见解析；（2）详见解析；（3）
.
【解析】
（1）由M、N是PA、PB中点，结合三角形中位线定理得MN∥AB，从而MN∥CD，由线面平行的判定定理证得MN∥平面PDC；（2）由DN⊥PB，
，利用线面垂直判定定理得直线DN⊥平面PBC；（3）用等体积法，求VP﹣ABC相应的高PD和底面积，再用体积公式即可．
（1）证明：连接
，∵
是
中点，∴
，从而
．
∵
在平面
外，
在平面内，∴直线
平面；
（2）证明：∵
，∴
．
∵
底面
，直线
与底面成
角，
∴
．∴
．
∵
是
的中点，∴
．
∵
， ∴．
∵
相交于一点，∴直线
平面
；
（3）
．
【题目】（Ⅰ）如表所示是某市最近5年个人年平均收入表节选．求y关于x的回归直线方程，并估计第6年该市的个人年平均收入（保留三位有效数字）．
年份x | 1 | 2 | 3 | 4 | 5 |
收入y（千元） | 21 | 24 | 27 | 29 | 31 |
其中
，
，
附1：
= ，=﹣
（Ⅱ）下表是从调查某行业个人平均收入与接受专业培训时间关系得到2×2列联表：
受培时间一年以上 | 受培时间不足一年 | 总计 | |
收入不低于平均值 | 60 | 20 | |
收入低于平均值 | 10 | 20 | |
总计 | 100 |
完成上表，并回答：能否在犯错概率不超过0.05的前提下认为“收入与接受培训时间有关系”．
附2：
P（K2≥k0） | 0.50 | 0.40 | 0.10 | 0.05 | 0.01 | 0.005 |
k0 | 0.455 | 0.708 | 2.706 | 3.841 | 6.635 | 7.879 |
附3：
K2=．（n=a+b+c+d）
【题目】已知某中学高三文科班学生共有800人参加了数学与地理的水平测试，学校决定利用随机数表法从中抽取100人进行成绩抽样调查，先将800人按001，002，…，800进行编号．
（1）如果从第8行第7列的数开始向右读，请你依次写出最先检查的3个人的编号；（下面摘取了第7行到第9行）
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 56 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
（2）抽取的100人的数学与地理的水平测试成绩如下表：
人 数 | 数 学 | |||
优 秀 | 良 好 | 及 格 | ||
地 理 | 优 秀 | 7 | 20 | 5 |
良 好 | 9 | 18 | 6 | |
及 格 | a | 4 | b | |
成绩分为优秀、良好、及格三个等级；横向、纵向分别表示地理成绩与数学成绩，例如：表中数学成绩为良好的共有
．
①若在该样本中，数学成绩优秀率是
，求
的值：
②在地理成绩及格的学生中，已知
，
，求数学成绩优秀的人数比及格的人数少的概率．
