题目内容
【题目】如图,在四棱锥P﹣ABCD中,四边形ABCD为平行四边形,AC,BD相交于点O,点E为PC的中点,OP=OC,PA⊥PD.求证: 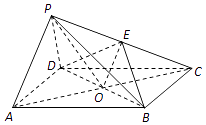
(1)直线PA∥平面BDE;
(2)平面BDE⊥平面PCD.
【答案】
(1)证明:连结OE,因为O为平行四边形ABCD对角线的交点,所以O为AC中点.
又因为E为PC的中点,
所以OE∥PA.
又因为OE平面BDE,PA平面BDE,
所以直线PA∥平面BDE
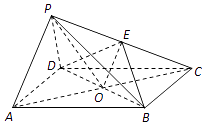
(2)证明:因为OE∥PA,PA⊥PD,所以OE⊥PD.
因为OP=OC,E为PC的中点,所以OE⊥PC.
又因为PD平面PCD,PC平面PCD,PC∩PD=P,
所以OE⊥平面PCD.
又因为OE平面BDE,所以平面BDE⊥平面PCD..
【解析】(1)连结OE,说明OE∥PA.然后证明PA∥平面BDE.(2)证明OE⊥PD.OE⊥PC.推出OE⊥平面PCD.然后证明平面BDE⊥平面PCD.
【考点精析】本题主要考查了直线与平面平行的判定和平面与平面垂直的判定的相关知识点,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一个平面过另一个平面的垂线,则这两个平面垂直才能正确解答此题.

练习册系列答案
相关题目
【题目】为调查乘客的候车情况,公交公司在某为台的![]() 名候车乘客中随机抽取
名候车乘客中随机抽取![]() 人,将他们的候车时间(单位:分钟)作为样本分成
人,将他们的候车时间(单位:分钟)作为样本分成![]() 组,如下表所示:
组,如下表所示:
组别 | 候车时间 | 人数 |
一 |
|
|
二 |
|
|
三 |
|
|
四 |
|
|
五 |
|
|
(1)求这![]() 名乘客的平均候车时间;
名乘客的平均候车时间;
(2)估计这![]() 名候车乘客中候车时间少于
名候车乘客中候车时间少于![]() 分钟的人数;
分钟的人数;
(3)若从上表第三、四组的![]() 人中随机抽取
人中随机抽取![]() 人作进一步的问卷调查,求抽到的两人恰好来自不同组的概率.
人作进一步的问卷调查,求抽到的两人恰好来自不同组的概率.