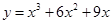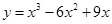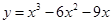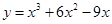题目内容
已知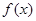 为奇函数,且
为奇函数,且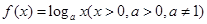 ,则当
,则当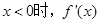 =( )
=( )
A.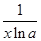 | B.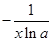 | C. | D.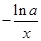 |
B
解析试题分析:由题意,可先由函数是奇函数的性质解出x<0时函数的解析式,再由求导公式解f′(x)的表达式即可得到正确选项解:∵f(x)为奇函数,且f(x)= (x>0,a>0,a≠1),任取x<0,则-x>0,∴f(-x)=loga(-x),又f(x)为奇函数,∴f(-x)=-f(x),∴f(x)=-
(x>0,a>0,a≠1),任取x<0,则-x>0,∴f(-x)=loga(-x),又f(x)为奇函数,∴f(-x)=-f(x),∴f(x)=- ,∴
,∴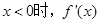 =
=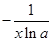 ,选B.
,选B.
考点:导数的运算公式及函数奇偶性
点评:本题考查了导数的运算公式及函数奇偶性的性质,解题的关键是熟练记忆导数公式及利用函数奇偶性求出x<0时函数的解析式,本题是函数性质考查的基本题型,难度较底

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
已知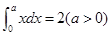 ,则
,则 的值为( )
的值为( )
| A.1 | B.2 | C.3 | D.4 |
设曲线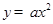 在点
在点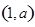 处的切线与直线
处的切线与直线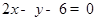 平行,则
平行,则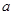 =( )
=( )
A.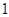 ; ; | B.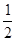 ; ; | C.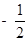 ; ; | D.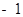 |
已知 是定义在
是定义在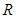 上的函数,若
上的函数,若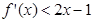 且
且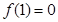 ,则
,则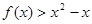 的解集为( )
的解集为( )
A.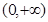 | B.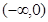 | C.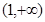 | D.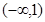 |
一质点做直线运动,由始点经过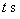 后的距离为
后的距离为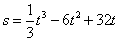 ,则速度为
,则速度为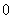 的时刻是( )
的时刻是( )
A.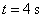 | B.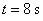 | C.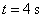 与 与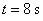 | D.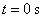 与 与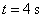 |
设函数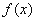 在
在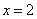 处导数存在,则
处导数存在,则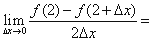 ( )
( )
A.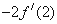 | B.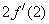 | C.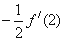 | D.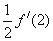 |
若定义在R上的函数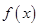 的导函数是
的导函数是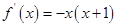 ,则函数
,则函数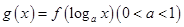 的单调递减区间是( )
的单调递减区间是( )
A.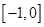 | B.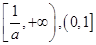 | C.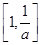 | D.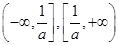 |
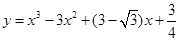 上移动,经过点P的切线的倾斜角为
上移动,经过点P的切线的倾斜角为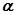 ,则角
,则角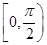
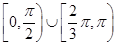


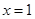 是有极大值4,当
是有极大值4,当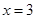 是有极小值0,且函数过原点,则此函数是( )
是有极小值0,且函数过原点,则此函数是( )