题目内容
设函数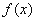 在
在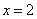 处导数存在,则
处导数存在,则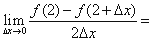 ( )
( )
A.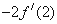 | B.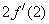 | C.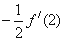 | D.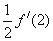 |
C
解析试题分析:根据题意,由于函数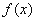 在
在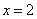 处导数存在,则
处导数存在,则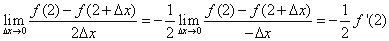 ,故可知答案为C.
,故可知答案为C.
考点:导数的定义
点评:本题主要考查了导数的定义,以及极限及其运算,属于基础题.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
设 是可导函数,且
是可导函数,且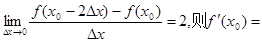 ( )
( )
A.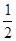 | B.-1 | C.0 | D.-2 |
已知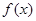 为奇函数,且
为奇函数,且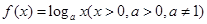 ,则当
,则当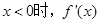 =( )
=( )
A.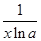 | B.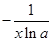 | C. | D.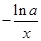 |
已知二次函数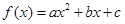 的导数为
的导数为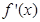 ,
,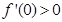 ,对于任意实数
,对于任意实数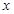 都有
都有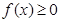 ,则
,则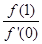 的最小值为 ( )
的最小值为 ( )
A.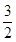 | B.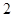 | C.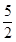 | D.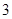 |
已知对任意实数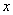 ,有
,有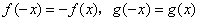 ,且
,且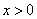 时,
时,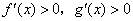 ,则
,则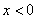 时
时
A.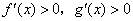 | B.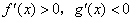 |
C.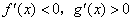 | D.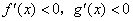 |
函数f(x)的定义域为开区间(a,b),导函数f′(x)在(a,b)内的图象如图所示,则函数f(x)在开区间(a,b)内有极小值点( )
| A.1个 | B.2个 |
| C.3个 | D.4个 |
已知曲线y= x2-2上一点P
x2-2上一点P ,则过点P的切线的方程是( )
,则过点P的切线的方程是( )
A.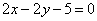 | B.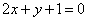 |
C.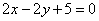 | D.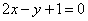 |
设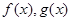 分别是定义在
分别是定义在 上的奇函数和偶函数,当
上的奇函数和偶函数,当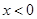 时,
时, 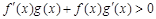 ,且
,且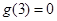 ,则不等式
,则不等式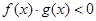 的解集是( )
的解集是( )
| A.(-3,0)∪(3,+∞) | B.(-3,0)∪(0, 3) |
| C.(-∞,- 3)∪(3,+∞) | D.(-∞,- 3)∪(0, 3) |
函数 的单调递增区间是
的单调递增区间是
A. | B.(0,3) | C.(1,4) | D. |