题目内容
7.已知不等式2x-1>m(x2-1),是否存在实数m,使不等式对任意x∈R恒成立?并说明理由.分析 利用一元二次不等式的性质,进行判断求解即可.
解答 解:∵2x-1>m(x2-1),
∴mx2-2x+1-m<0,
若m=0,则不等式等价为-2x+1<0,解得x>$\frac{1}{2}$,不满足条件.
若mx2-2x+1-m<0恒成立,
则满足$\left\{\begin{array}{l}{m<0}\\{△=4-4m(1-m)<0}\end{array}\right.$,
即$\left\{\begin{array}{l}{m<0}\\{{m}^{2}-m-1<0}\end{array}\right.$,
即$\left\{\begin{array}{l}{m<0}\\{\frac{1-\sqrt{5}}{2}<m<\frac{1+\sqrt{5}}{2}}\end{array}\right.$,
解得$\frac{1-\sqrt{5}}{2}$<m<0,
即存在$\frac{1-\sqrt{5}}{2}$<m<0使不等式对任意x∈R恒成立.
点评 本题主要考查不等式恒成立问题,根据一元二次不等式和判别式△之间的关系是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.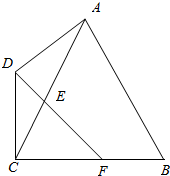 如图所示,平面四边形ABCD中,AB=AC=BC=$\sqrt{3}$,CD=AD=1,已知$\overrightarrow{AE}$=$λ\overrightarrow{AC}$,$\overrightarrow{CF}$=λ$\overrightarrow{CB}$,λ∈(0,1),且存在实数t使$\overrightarrow{CE}$=t$\overrightarrow{CD}$+(1-t)$\overrightarrow{CF}$,则$\overrightarrow{EA}$•$\overrightarrow{AB}$=( )
如图所示,平面四边形ABCD中,AB=AC=BC=$\sqrt{3}$,CD=AD=1,已知$\overrightarrow{AE}$=$λ\overrightarrow{AC}$,$\overrightarrow{CF}$=λ$\overrightarrow{CB}$,λ∈(0,1),且存在实数t使$\overrightarrow{CE}$=t$\overrightarrow{CD}$+(1-t)$\overrightarrow{CF}$,则$\overrightarrow{EA}$•$\overrightarrow{AB}$=( )
 如图所示,平面四边形ABCD中,AB=AC=BC=$\sqrt{3}$,CD=AD=1,已知$\overrightarrow{AE}$=$λ\overrightarrow{AC}$,$\overrightarrow{CF}$=λ$\overrightarrow{CB}$,λ∈(0,1),且存在实数t使$\overrightarrow{CE}$=t$\overrightarrow{CD}$+(1-t)$\overrightarrow{CF}$,则$\overrightarrow{EA}$•$\overrightarrow{AB}$=( )
如图所示,平面四边形ABCD中,AB=AC=BC=$\sqrt{3}$,CD=AD=1,已知$\overrightarrow{AE}$=$λ\overrightarrow{AC}$,$\overrightarrow{CF}$=λ$\overrightarrow{CB}$,λ∈(0,1),且存在实数t使$\overrightarrow{CE}$=t$\overrightarrow{CD}$+(1-t)$\overrightarrow{CF}$,则$\overrightarrow{EA}$•$\overrightarrow{AB}$=( )| A. | $\frac{\sqrt{3}}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | -$\frac{3}{4}$ | D. | -1 |