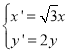题目内容
【题目】已知椭圆
的离心率为
，点
在
上.
（1） 求椭圆的方程；
（2） 设
分别是椭圆的上、下焦点，过
的直线
与椭圆交于不同的两点
，求
的内切圆的半径的最大值．
【答案】（1）
；（2）
【解析】
（1）根据题意得e
，①因为点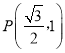
椭圆C上，所以
，②又b2＝a2﹣c2，③把①②③组成方程组，解得a，b，c，进而可以写出椭圆方程；
（2）因为
，所以
，所以
4a×r＝c×|
﹣
|，所以r
|﹣|，设直线l方程为y
kx
，A（x1，y1），B（x2，y2），联立直线l与椭圆的方程得（k2+4）x2﹣2
kx﹣1＝0，由韦达定理得出|﹣|的最大值，即可求出答案．
解：（1）根据题意得e，①
因为点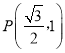在椭圆C上，所以，②
又b2＝a2﹣c2，③
把①②③组成方程组，解得a2＝4，b2＝1，c2＝3
所以椭圆方程为．
（2）设直线l方程为ykx， A（x1，y1），B（x2，y2），
因为，
所以，
所以4a×r＝c×|﹣|，
所以r
|﹣|，
联立直线l与椭圆的方程得（k2+4）x2﹣2 kx﹣1＝0，
所以
，
，
所以|﹣|
，
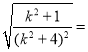＝4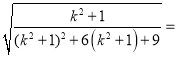
4
4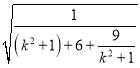
，
由基本不等式得（k2+1）
2
6（当且仅当
，即k2＝2，取“＝”），
所以|﹣|
，
rmax
．
名校课堂系列答案
【题目】某城市有东、西、南、北四个进入城区主干道的入口，在早高峰时间段，时常发生交通拥堵，交警部门记录了11月份30天内的拥堵情况（如下表所示，其中●表示拥堵，○表示通畅）.假设每个人口是否发生拥堵相互独立，将各入口在这30天内拥堵的频率代替各入口每天拥堵的概率.
11.1 | 11.2 | 11.3 | 11.4 | 11.5 | 11.6 | 11.7 | 11.8 | 11.9 | 11.10 | 11.11 | 11.12 | 11.13 | 11.14 | 11.15 | ||||||||||||||||
东入口 | ● | ○ | ○ | ○ | ○ | ● | ○ | ● | ● | ○ | ● | ● | ● | ○ | ● | |||||||||||||||
西入口 | ○ | ○ | ● | ● | ○ | ● | ○ | ● | ○ | ● | ○ | ● | ● | ○ | ○ | |||||||||||||||
南入口 | ○ | ● | ○ | ○ | ○ | ● | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ● | |||||||||||||||
北入口 | ● | ○ | ○ | ○ | ● | ○ | ○ | ● | ○ | ○ | ○ | ○ | ○ | ● | ○ | |||||||||||||||
11.16 | 11.17 | 11.18 | 11.19 | 11.20 | 11.21 | 11.22 | 11.23 | 11.24 | 11.25 | 11.26 | 11.27 | 11.28 | 11.29 | 11.30 | ||||||||||||||||
东入口 | ● | ○ | ○ | ● | ○ | ○ | p>○ | ● | ● | ○ | ● | ○ | ● | ○ | ● | |||||||||||||||
西入口 | ● | ○ | ● | ● | ○ | ● | ○ | ● | ○ | ● | ○ | ● | ○ | ● | ○ | |||||||||||||||
南入口 | ○ | ○ | ○ | ● | ○ | ○ | ○ | ○ | ● | ○ | ○ | ○ | ○ | ○ | ● | |||||||||||||||
北入口 | ○ | ○ | ● | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ● | ○ | |||||||||||||||
（1）分别求该城市一天中早高峰时间段这四个主干道的入口发生拥堵的概率.
（2）各人口一旦出现拥堵就需要交通协管员来疏通，聘请交通协管员有以下两种方案可供选择.方案一：四个主干道入口在早高峰时间段每天各聘请一位交通协管员，聘请每位交通协管员的日费用为
（
，且
）元.方案二：在早高峰时间段若某主干道入口发生拥堵，交警部门则需临时调派两位交通协管员协助疏通交通，调派后当日需给每位交通协管员的费用为200元.以四个主干道入口聘请交通协管员的日总费用的数学期望为依据，你认为在这两个方案中应该如何选择？请说明理由.
