题目内容
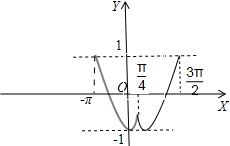
 已知定义在区间[-π,
已知定义在区间[-π,| 3π |
| 2 |
| π |
| 4 |
| π |
| 4 |
(1)作出y=f(x)的图象;
(2)求y=f(x)的解析式;
(3)当a∈[-1,1]时,讨论关于x的方程f(x)=a的解的个数.
分析:(1)、先根据当 x≥
时,f(x)=-sinx画出在[
,
]上的图象;再根据图象关于直线x=
对称把另一部分添上即可;
(2)先根据x∈[-π,
],得
-x∈[
,
],再结合当x≥
时,f(x)=-sinx即可求出y=f(x)的解析式;
(3)结合图象可得:关于x的方程f(x)=a有解可以分为四个根,三个根,两个根三种情况.
| π |
| 4 |
| π |
| 4 |
| 3π |
| 2 |
| π |
| 4 |
(2)先根据x∈[-π,
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| 3π |
| 2 |
| π |
| 4 |
(3)结合图象可得:关于x的方程f(x)=a有解可以分为四个根,三个根,两个根三种情况.
解答:解:(1)、y=f(x)的图象如图所示.
(2)、任取x∈[-π,
],则
-x∈[
,
],因为函数y=f(x)图象关于直线x=
对称,
则f(x)=f(
-x),
又当x≥
时,f(x)=-sinx,则f(x)=f(
-x)=-sin(
-x)=-cosx,
即f(x)=
.
(3)、由(1)可知:
当a=-
,方程3解.
当a∈(-1,-
)时,方程4解.
当a∈{a|-
<a≤1或a=-1}时,方程2解

(2)、任取x∈[-π,
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| 3π |
| 2 |
| π |
| 4 |
则f(x)=f(
| π |
| 2 |
又当x≥
| π |
| 4 |
| π |
| 2 |
| π |
| 2 |
即f(x)=
|
(3)、由(1)可知:
当a=-
| ||
| 2 |
当a∈(-1,-
| ||
| 2 |
当a∈{a|-
| ||
| 2 |
点评:本题主要考查分段函数的解析式求法及其图象的作法以及分类讨论思想的运用.解决第二问的关键在于根据x∈[-π,
]得到
-x∈[
,
].
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| 3π |
| 2 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
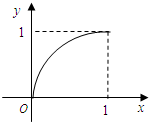 已知定义在区间[0,1]上的函数y=f(x)的图象如图所示,对于满足0<x1<x2<1的任意x1,x2,给出下列结论:
已知定义在区间[0,1]上的函数y=f(x)的图象如图所示,对于满足0<x1<x2<1的任意x1,x2,给出下列结论: