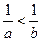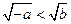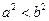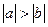题目内容
设a∈R,f(x)=
是奇函数,
(1)求a的值;
(2)如果g(n)=
(n∈N+),试比较f(n)与g(n)的大小(n∈N+).
| a•2x+a-2 |
| 2x+1 |
(1)求a的值;
(2)如果g(n)=
| n |
| n+1 |
∵(1)f(x)是定义在R上的奇函数,∴f(0)=0,2a-2=0,解得a=1.
经验证a=1,f(x)是奇函数,∴a=1.
(2)由(1)可知:f(x)=
,∴f(n)=
.
∴f(n)-g(n)=
-
=
.
只要比较2n与2n+1的大小即可.
当n=1,2时,f(n)<g(n);当n≥3时,2n>2n+1,f(n)>g(n).
下面证明,n≥3时,2n>2n+1,即f(x)>g(x).
①n=3时,23>2×3+1,显然成立,
②假设n=k(k≥3,k∈N+)时,2k>2k+1,
那么n=k+1时,2k+1=2×2k>2(2k+1).
2(2k+1)-[2(k+1)+1]=4k+2-2k-3=2k-1>0(∵k≥3),
有2k+1>2(k+1)+1.
∴n=k+1时,不等式也成立,由①②可以断定,n≥3,n∈N+时,2n>2n+1.
结论:n=1,2时,f(n)<g(n);当n≥3,n∈N+时,f(n)>g(n).
经验证a=1,f(x)是奇函数,∴a=1.
(2)由(1)可知:f(x)=
| 2x-1 |
| 2x+1 |
| 2n-1 |
| 2n+1 |
∴f(n)-g(n)=
| 2n-1 |
| 2n+1 |
| n |
| n+1 |
| 2n-2n-1 |
| (2n+1)(n+1) |
只要比较2n与2n+1的大小即可.
当n=1,2时,f(n)<g(n);当n≥3时,2n>2n+1,f(n)>g(n).
下面证明,n≥3时,2n>2n+1,即f(x)>g(x).
①n=3时,23>2×3+1,显然成立,
②假设n=k(k≥3,k∈N+)时,2k>2k+1,
那么n=k+1时,2k+1=2×2k>2(2k+1).
2(2k+1)-[2(k+1)+1]=4k+2-2k-3=2k-1>0(∵k≥3),
有2k+1>2(k+1)+1.
∴n=k+1时,不等式也成立,由①②可以断定,n≥3,n∈N+时,2n>2n+1.
结论:n=1,2时,f(n)<g(n);当n≥3,n∈N+时,f(n)>g(n).

练习册系列答案
相关题目
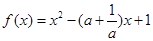 .
.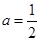 时,解不等式
时,解不等式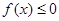 ;
;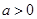 ,解关于
,解关于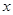 的不等式
的不等式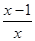 ≥1的解集为( )
≥1的解集为( )