题目内容
已知a1,a2,…,an;b1,b2,…,bn(n是正整数),令L1=b1+b2+…+bn,L2=b2+b3+…+bn,…,Ln=bn、某人用右图分析得到恒等式:a1b1+a2b2+…+anbn=a1L1+c2L2+c3L3+…+ckLk+…+…+cnLn,则ck= (2≤k≤n).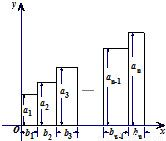
【答案】分析:首先分析题目已知a1b1+a2b2+…+anbn=a1L1+c2L2+c3L3+…+ckLk+…+…+cnLn,可以看出等式左边是图中的面积,然后把左边变换形式后等于右边即可得到答案.
解答:解:因为已知恒等式a1b1+a2b2+…+anbn=a1L1+c2L2+c3L3+…+ckLk+…+…+cnLn
且L1=b1+b2+…+bn,L2=b2+b3+…+bn,…,Ln=bn、
又由图中的面积S=a1b1+a2b2+…+anbn
=a1(b1+b2+b3+…+bn)+(a2-a1)(b2+b3+…+bn)+…+(an-1-an-2)(bn-1+bn)+(an-an-1)bn
=a1L1+(a2-a1)L2+…+(an-1-an-2)Ln-1+(an-an-1)Ln
所以ck=ak-ak-1
点评:此题主要考查柯西不等式的几何意义,题目看似无头绪,仔细分析等式后变形化简即可很容易解得答案,有一定的技巧性,同学们做题时候需要仔细分析.
解答:解:因为已知恒等式a1b1+a2b2+…+anbn=a1L1+c2L2+c3L3+…+ckLk+…+…+cnLn
且L1=b1+b2+…+bn,L2=b2+b3+…+bn,…,Ln=bn、
又由图中的面积S=a1b1+a2b2+…+anbn
=a1(b1+b2+b3+…+bn)+(a2-a1)(b2+b3+…+bn)+…+(an-1-an-2)(bn-1+bn)+(an-an-1)bn
=a1L1+(a2-a1)L2+…+(an-1-an-2)Ln-1+(an-an-1)Ln
所以ck=ak-ak-1
点评:此题主要考查柯西不等式的几何意义,题目看似无头绪,仔细分析等式后变形化简即可很容易解得答案,有一定的技巧性,同学们做题时候需要仔细分析.

练习册系列答案
相关题目
已知
,
均为单位向量,那么
=(
,
)是
+
=(
,1)的( )
| a1 |
| a2 |
| a1 |
| ||
| 2 |
| 1 |
| 2 |
| a1 |
| a2 |
| 3 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分又不必要条件 |