题目内容
已知
,
均为单位向量,那么
=(
,
)是
+
=(
,1)的( )
| a1 |
| a2 |
| a1 |
| ||
| 2 |
| 1 |
| 2 |
| a1 |
| a2 |
| 3 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分又不必要条件 |
分析:通过举反例可以看出,当
=(
,
)时,不能推出
+
=(
,1),当
+
=(
,1) 时,
+
的模为2,均由于
,
均为单位向量,
,
是同向的两个向量,故有
=(
,
)=
.再利用充分条件、必要条件的定义进行判断.
| a1 |
| ||
| 2 |
| 1 |
| 2 |
| a1 |
| a2 |
| 3 |
| a1 |
| a2 |
| 3 |
| a1 |
| a2 |
| a1 |
| a2 |
| a1 |
| a2 |
| a1 |
| ||
| 2 |
| 1 |
| 2 |
| a2 |
解答:解:由于
,
均为单位向量,当
=(
,
)时,不能推出
+
=(
,1),
若
=-
,则
+
=(
,0).
当
+
=(
,1) 时,
+
的模为2,均由于
,
均为单位向量,∴
∥
,且是同向的.
能推出
=(
,
)=
.
故
=(
,
)是
+
=(
,1)的 必要不充分条件,故选 B.
| a1 |
| a2 |
| a1 |
| ||
| 2 |
| 1 |
| 2 |
| a1 |
| a2 |
| 3 |
若
| a2 |
| a1 |
| a1 |
| a2 |
| 0 |
当
| a1 |
| a2 |
| 3 |
| a1 |
| a2 |
| a1 |
| a2 |
| a1 |
| a2 |
能推出
| a1 |
| ||
| 2 |
| 1 |
| 2 |
| a2 |
故
| a1 |
| ||
| 2 |
| 1 |
| 2 |
| a1 |
| a2 |
| 3 |
点评:本题考查单位向量的定义,两个向量坐标形式的运算,充分条件、必要条件、充要条件的定义.

练习册系列答案
相关题目
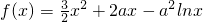 ,二次函数g(x)=ax2-2x+1.
,二次函数g(x)=ax2-2x+1.