题目内容
如图,已知△OFQ的面积为S,且 ·
· =1.设|
=1.设| |=c(c≥2),S=
|=c(c≥2),S=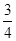 c.若以O为中心,F为一个焦点的椭圆经过点Q,当|
c.若以O为中心,F为一个焦点的椭圆经过点Q,当| |取最小值时,求椭圆的方程.
|取最小值时,求椭圆的方程.

 ·
· =1.设|
=1.设| |=c(c≥2),S=
|=c(c≥2),S=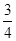 c.若以O为中心,F为一个焦点的椭圆经过点Q,当|
c.若以O为中心,F为一个焦点的椭圆经过点Q,当| |取最小值时,求椭圆的方程.
|取最小值时,求椭圆的方程.
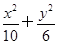 =1
=1以O为原点, 所在直线为x轴建立平面直角坐标系.设椭圆方程为
所在直线为x轴建立平面直角坐标系.设椭圆方程为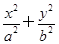 =1(a>b>0),Q(x,y).
=1(a>b>0),Q(x,y). =(c,0),则
=(c,0),则 =(x-c,y).∵
=(x-c,y).∵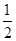 |
| |·y=
|·y=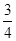 c,∴y=
c,∴y=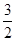 .
.
又∵ ·
· =c(x-c)=1,∴x=c+
=c(x-c)=1,∴x=c+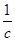 .则|
.则| |=
|=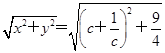 (c≥2).
(c≥2).
可以证明:当c≥2时,函数t=c+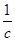 为增函数,
为增函数,
∴当c=2时,| |min=
|min=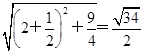 ,此时Q
,此时Q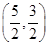 .将Q的坐标代入椭圆方程,得
.将Q的坐标代入椭圆方程,得 解得
解得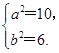 ∴椭圆方程为
∴椭圆方程为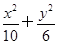 =1.
=1.
 所在直线为x轴建立平面直角坐标系.设椭圆方程为
所在直线为x轴建立平面直角坐标系.设椭圆方程为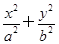 =1(a>b>0),Q(x,y).
=1(a>b>0),Q(x,y). =(c,0),则
=(c,0),则 =(x-c,y).∵
=(x-c,y).∵ |
| |·y=
|·y=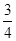 c,∴y=
c,∴y=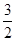 .
.又∵
 ·
· =c(x-c)=1,∴x=c+
=c(x-c)=1,∴x=c+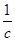 .则|
.则| |=
|=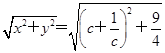 (c≥2).
(c≥2).可以证明:当c≥2时,函数t=c+
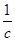 为增函数,
为增函数,∴当c=2时,|
 |min=
|min=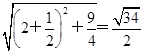 ,此时Q
,此时Q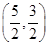 .将Q的坐标代入椭圆方程,得
.将Q的坐标代入椭圆方程,得 解得
解得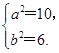 ∴椭圆方程为
∴椭圆方程为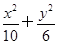 =1.
=1.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (a>b>0)的上、下顶点分别为A、B,已知点B在直线l:
(a>b>0)的上、下顶点分别为A、B,已知点B在直线l: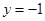 上,且椭圆的离心率e =
上,且椭圆的离心率e =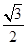 .
.
 ,它的一个顶点恰好是抛物线
,它的一个顶点恰好是抛物线 的焦点.
的焦点.
 APQ=
APQ= 为椭圆
为椭圆 右焦点,圆
右焦点,圆 与椭圆
与椭圆 的一个公共点为
的一个公共点为 ,且直线
,且直线 与圆
与圆 相切与点
相切与点 。
。
 的值及椭圆
的值及椭圆 满足
满足 ,其中
,其中 是椭圆
是椭圆 为原点,直线
为原点,直线 与
与 的斜率之积为
的斜率之积为 ,求证:
,求证: 为定值。
为定值。 +
+ =1(a>b>0),以抛物线y2=8x的焦点为顶点,且离心率为
=1(a>b>0),以抛物线y2=8x的焦点为顶点,且离心率为 .
. =
= +
+ ,证明
,证明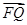 为定值,并求出该值.
为定值,并求出该值. =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,其左焦点到点P(2,1)的距离为
,其左焦点到点P(2,1)的距离为 .不过原点O的直线l与C相交于A,B两点,且线段AB被直线OP平分.
.不过原点O的直线l与C相交于A,B两点,且线段AB被直线OP平分.
 =1(a>b>0)的左、右焦点,A,B分别是椭圆E的左、右顶点,且
=1(a>b>0)的左、右焦点,A,B分别是椭圆E的左、右顶点,且 +5
+5 =0.
=0.
 =1(a>b>0)的左、右焦点,点M在x轴上,且
=1(a>b>0)的左、右焦点,点M在x轴上,且 =
=
 ,过点F2的直线与椭圆交于A、B两点,且AM⊥x轴,
,过点F2的直线与椭圆交于A、B两点,且AM⊥x轴, ·
·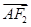 =0.
=0.
 ,求椭圆的方程.
,求椭圆的方程. =1(a>b>0)的焦距为2c,以O为圆心,a为半径的圆.过点
=1(a>b>0)的焦距为2c,以O为圆心,a为半径的圆.过点 作圆的两切线互相垂直,则离心率e=________.
作圆的两切线互相垂直,则离心率e=________.