题目内容
口袋里装有大小相同的4个红球和8个白球,甲、乙两人依规则从袋中有放回摸球,每次摸出一个球.规则:若一方摸出红球,则此人继续摸球;若一方摸出白球,则由对方下一次摸球.每次摸球都相互独立,并由甲先进行第一次摸球.
(1)求第三次由甲摸球的概率;
(2)写出在前三次摸球中,甲摸得红球的次数的分布列,并求数学期望.
(1)求第三次由甲摸球的概率;
(2)写出在前三次摸球中,甲摸得红球的次数的分布列,并求数学期望.
分析:(1)根据题意可得:事件“第三次由甲摸球”包含以下两种情况:①甲前2次都摸到红球,则第3次仍然由甲摸球,②甲首先摸到白球,乙再摸到白球,而第3次则由甲摸球,再分别根据题意与相互独立事件的概率乘法公式求出其发生的概率即可得到答案.
(2)设甲摸到红球的次数为ξ,根据题意知ξ的可能取值为0,1,2,3,再结合题意与相互独立事件的概率乘法公式分别求出其发生的概率,进而算出ξ的数学期望.
(2)设甲摸到红球的次数为ξ,根据题意知ξ的可能取值为0,1,2,3,再结合题意与相互独立事件的概率乘法公式分别求出其发生的概率,进而算出ξ的数学期望.
解答:解:(1)根据题意可得:事件“第三次由甲摸球”包含以下两种情况:①甲前2次都摸到红球,则第3次仍然由甲摸球,并且其概率为:
;
②甲首先摸到白球,乙再摸到白球,而第3次则由甲摸球,并且其概率为:
,
所以P(第三次由甲摸球)=
+
=
…(5分)
(2)记“甲摸球一次摸出红球”为事件A“乙摸球一次摸出红球”为事件B,
则 P(A)=P(B)=
=
,P(
)=P(
)=
,并且根据题意可得:A,B是相互独立事件.
设甲摸到红球的次数为ξ,根据题意知ξ的可能取值为0,1,2,3,
所以P(ξ=0)=P(
•B)+P(
•
•
)=
×
+(
)3=
,P(ξ=1)=P(A•
)+P(
•
•A)=
×
+(
)2×
=
,
P(ξ=2)=P(A•A•
)=(
)2×
=
,P(ξ=3)=P(A•A•A)=(
)3=
.
∴ξ的分布列为
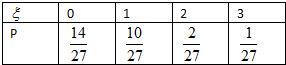
∴数学期望 Eξ=0×
+1×
+2×
+3×
=
.
| 1 |
| 9 |
②甲首先摸到白球,乙再摸到白球,而第3次则由甲摸球,并且其概率为:
| 4 |
| 9 |
所以P(第三次由甲摸球)=
| 1 |
| 9 |
| 4 |
| 9 |
| 5 |
| 9 |
(2)记“甲摸球一次摸出红球”为事件A“乙摸球一次摸出红球”为事件B,
则 P(A)=P(B)=
| 4 |
| 4+8 |
| 1 |
| 3 |
. |
| A |
. |
| B |
| 2 |
| 3 |
设甲摸到红球的次数为ξ,根据题意知ξ的可能取值为0,1,2,3,
所以P(ξ=0)=P(
. |
| A |
. |
| A |
. |
| B |
. |
| A |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 14 |
| 27 |
. |
| A |
. |
| A |
. |
| B |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 10 |
| 27 |
P(ξ=2)=P(A•A•
. |
| A |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 27 |
| 1 |
| 3 |
| 1 |
| 27 |
∴ξ的分布列为

∴数学期望 Eξ=0×
| 14 |
| 27 |
| 10 |
| 27 |
| 2 |
| 27 |
| 1 |
| 27 |
| 17 |
| 27 |
点评:解决此类问题的关键是熟练掌握相互独立事件的概率乘法公式,以及离散型随机变量的分布列与数学期望,此题属于中档题,是近几年高考命题的热点之一.

练习册系列答案
相关题目