题目内容
以下四个命题:①¬q是¬p的必要不充分条件,则p是q的充分不必要条件;
②和定点A(5,0)及定直线
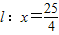 的距离之比为
的距离之比为 的点的轨迹方程为
的点的轨迹方程为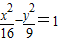 ;
;③当d无限趋近于0时,
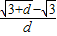 无限趋近于
无限趋近于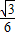 ;
;④设点F1(0,-3),F2(0,3),点P满足
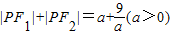 ,则点P的轨迹为椭圆;
,则点P的轨迹为椭圆;其中真命题为 (写出所以真命题的序号).
【答案】分析:①根据互为逆否命题的命题的真假相同可判断
②由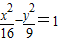 的右焦点为(5,0),右准线为x=
的右焦点为(5,0),右准线为x=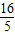 ,离心率e=
,离心率e= ,根据圆锥曲线的定义可判断
,根据圆锥曲线的定义可判断
③当d无限趋近于0时,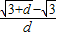 =
=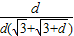 =
=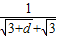 可判断
可判断
④由a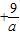 ≥6=F1F2,满足
≥6=F1F2,满足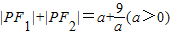 ≥F1F2,根据椭圆定义可判断
≥F1F2,根据椭圆定义可判断
解答:解:①根据互为逆否命题的命题的真假相同可知,¬q是¬p的必要不充分条件,则p是q的必要不充分条件;错误
②∵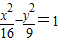 的右焦点为(5,0),右准线为x=
的右焦点为(5,0),右准线为x=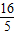 ,离心率e=
,离心率e= ,根据圆锥曲线的定义可知,和定点A(5,0)及定直线x=
,根据圆锥曲线的定义可知,和定点A(5,0)及定直线x=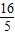 的距离之比为
的距离之比为 的点的轨迹方程为
的点的轨迹方程为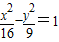 ;错误
;错误
③当d无限趋近于0时,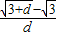 =
=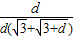 =
=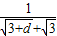 无限趋近于
无限趋近于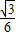 ;正确
;正确
④∵a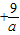 ≥6=F1F2,根据椭圆的定义可知,P满足
≥6=F1F2,根据椭圆的定义可知,P满足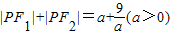 ,则点P的轨迹为椭圆或线段,故错误
,则点P的轨迹为椭圆或线段,故错误
故答案为:③
点评:本题主要考查了互为逆否命题的真假关系的应用,椭圆及双曲线的定义的应用.
②由
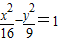 的右焦点为(5,0),右准线为x=
的右焦点为(5,0),右准线为x=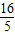 ,离心率e=
,离心率e= ,根据圆锥曲线的定义可判断
,根据圆锥曲线的定义可判断③当d无限趋近于0时,
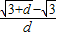 =
=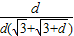 =
=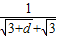 可判断
可判断④由a
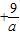 ≥6=F1F2,满足
≥6=F1F2,满足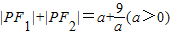 ≥F1F2,根据椭圆定义可判断
≥F1F2,根据椭圆定义可判断解答:解:①根据互为逆否命题的命题的真假相同可知,¬q是¬p的必要不充分条件,则p是q的必要不充分条件;错误
②∵
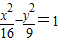 的右焦点为(5,0),右准线为x=
的右焦点为(5,0),右准线为x=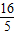 ,离心率e=
,离心率e= ,根据圆锥曲线的定义可知,和定点A(5,0)及定直线x=
,根据圆锥曲线的定义可知,和定点A(5,0)及定直线x=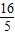 的距离之比为
的距离之比为 的点的轨迹方程为
的点的轨迹方程为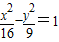 ;错误
;错误③当d无限趋近于0时,
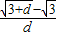 =
=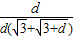 =
=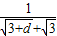 无限趋近于
无限趋近于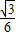 ;正确
;正确④∵a
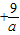 ≥6=F1F2,根据椭圆的定义可知,P满足
≥6=F1F2,根据椭圆的定义可知,P满足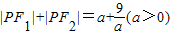 ,则点P的轨迹为椭圆或线段,故错误
,则点P的轨迹为椭圆或线段,故错误故答案为:③
点评:本题主要考查了互为逆否命题的真假关系的应用,椭圆及双曲线的定义的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目