题目内容
已知圆C:x2+y2-2ax-2(2a-1)y+4(a-1)=0,其中a∈R.
(1)证明:圆C过定点.
(2)当a变化时,求圆心轨迹方程.
(3)求面积最小的圆C的方程.
答案:
解析:
解析:
|
解:(1)将圆C方程化为x2+y2+2y-4+a(-2x-4y+4)=0. 令 所以不论a为何值,圆C经过两个定点A(2,0),B(- (2)设圆心C(x,y),则 (3)因为圆C恒过点A,B,所以当线段AB为直径时,圆C面积最小.S最小值=π |

练习册系列答案
相关题目
| |||||||||||
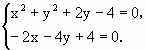 解得
解得 或
或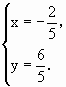
 ,
,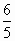 ).
). 消去a得y=2x-1.
消去a得y=2x-1. =
= π.所以圆C的方程为(x-
π.所以圆C的方程为(x-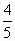 )2+(y-
)2+(y-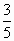 )2=
)2= .
.