题目内容
如图，函数F（x）=f（x）+| 1 |
| 5 |
考点：利用导数研究曲线上某点切线方程
专题：导数的综合应用
分析：由题意求得F（5）与F′（5），得到f（5）与f′（5），代入f（5）+f′（5）=-5求得a的值．
解答：
解：根据图象知，函数y=F（x）的图象与在点P处的切线交于点P，
F（5）=f（5）+5=5a+8，得f（5）=5a+3，
F′（5）为函数y=F（x）的图象在点P处的切线的斜率，
∴F′（5）=f′（5）+2=a，f′（5）=a-2，
由f（5）+f′（5）=-5，得5a+3+a-2=-5，解得：a=-1．
故答案为：-1．
F（5）=f（5）+5=5a+8，得f（5）=5a+3，
F′（5）为函数y=F（x）的图象在点P处的切线的斜率，
∴F′（5）=f′（5）+2=a，f′（5）=a-2，
由f（5）+f′（5）=-5，得5a+3+a-2=-5，解得：a=-1．
故答案为：-1．
点评：本题考查了利用导数研究过曲线上某点处的切线方程，过曲线上某点的切线的斜率，就是函数在该点处的导数值，是中档题．
练习册系列答案
名题训练系列答案
期末集结号系列答案
相关题目
若把函数 y=sin（x+
）的图象向右平移m（m＞0）个单位长度后，得到y=sinx的图象，则m的最小值（ ）
| π |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
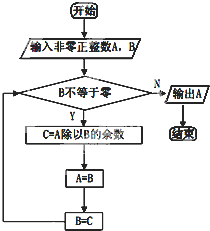在如图的算法中，如果输入A=138，B=22，则输出的结果是（ ）| A、2 | B、4 | C、128 | D、0 |
若角α的终边上有一点P（m，2m），（m＞0），则sinα的值是（ ）
A、
| ||||
B、-
| ||||
C、±
| ||||
| D、2 |