题目内容
(12分)
已知函数 (其中
(其中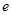 是自然对数的底数,
是自然对数的底数,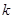 为正数)
为正数)
(I)若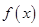 在
在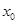 处取得极值,且
处取得极值,且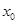 是
是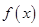 的一个零点,求
的一个零点,求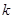 的值;
的值;
(II)若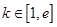 ,求
,求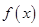 在区间
在区间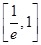 上的最大值;
上的最大值;
(III)设函数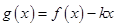 在区间
在区间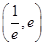 上是减函数,求
上是减函数,求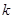 的取值范围.
的取值范围.
已知函数
 (其中
(其中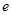 是自然对数的底数,
是自然对数的底数,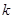 为正数)
为正数)(I)若
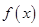 在
在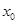 处取得极值,且
处取得极值,且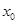 是
是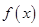 的一个零点,求
的一个零点,求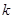 的值;
的值;(II)若
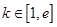 ,求
,求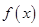 在区间
在区间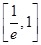 上的最大值;
上的最大值;(III)设函数
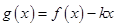 在区间
在区间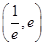 上是减函数,求
上是减函数,求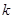 的取值范围.
的取值范围.(I)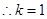
(II)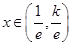 时,
时,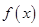 单调递减;
单调递减;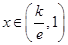 时,
时,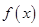 单调递增
单调递增
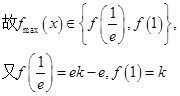
当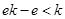 ,即
,即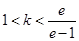 时,
时,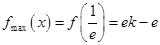
当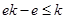 ,即
,即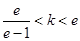 时,
时,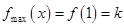
(III)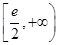
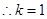
(II)
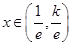 时,
时,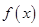 单调递减;
单调递减;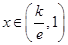 时,
时,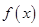 单调递增
单调递增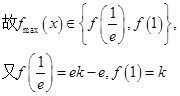
当
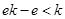 ,即
,即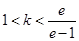 时,
时,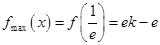
当
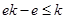 ,即
,即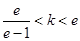 时,
时,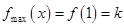
(III)
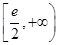
(I)由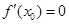 可得关于k的方程,解出k值.
可得关于k的方程,解出k值.
(II)先求导,然后利用导数研究f(x)的单调性极值和最值.
(III)本小题的实质是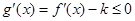 在区间
在区间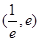 上恒成立,即
上恒成立,即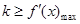 .
.
解法一:
(I)由已知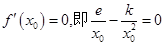
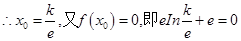
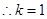
(II)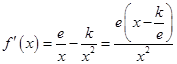
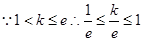
由此得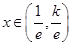 时,
时,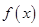 单调递减;
单调递减;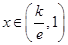 时,
时,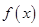 单调递增
单调递增
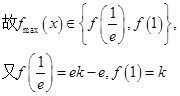
当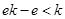 ,即
,即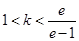 时,
时,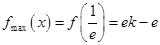
当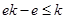 ,即
,即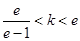 时,
时,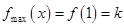
(III)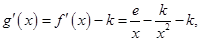
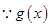 在
在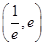 在是减函数,
在是减函数,
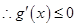 在
在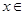
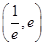 上恒成立
上恒成立
即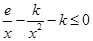 在
在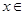
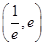 上恒成立
上恒成立
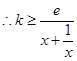 在
在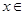
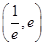 上恒成立
上恒成立
又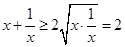 当且仅当
当且仅当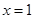 时等号成立.
时等号成立.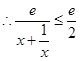
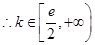
解法二;(I),(II)同解法一
(III)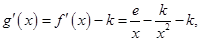
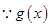
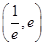 在是减函数,
在是减函数,
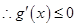 在
在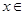
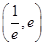 上恒成立
上恒成立
即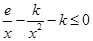 在
在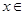
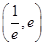 上恒成立
上恒成立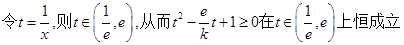
不妨设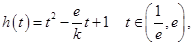
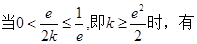
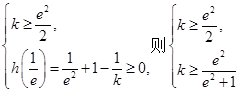
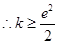
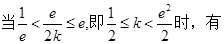
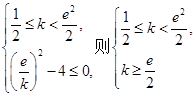
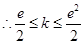
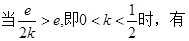
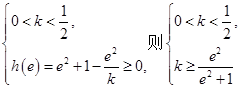
由于 无解.
无解.
综上所述,得出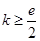 ,即
,即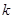 的取值范围是
的取值范围是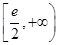
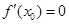 可得关于k的方程,解出k值.
可得关于k的方程,解出k值.(II)先求导,然后利用导数研究f(x)的单调性极值和最值.
(III)本小题的实质是
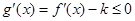 在区间
在区间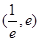 上恒成立,即
上恒成立,即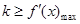 .
.解法一:
(I)由已知
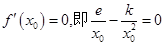
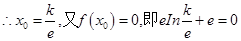
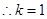
(II)
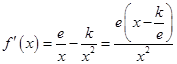
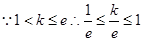
由此得
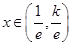 时,
时,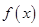 单调递减;
单调递减;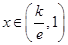 时,
时,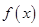 单调递增
单调递增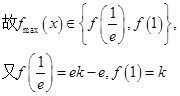
当
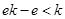 ,即
,即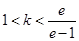 时,
时,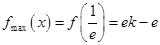
当
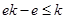 ,即
,即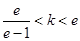 时,
时,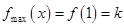
(III)
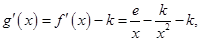
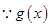 在
在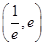 在是减函数,
在是减函数,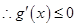 在
在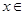
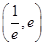 上恒成立
上恒成立即
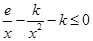 在
在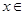
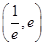 上恒成立
上恒成立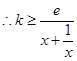 在
在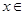
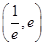 上恒成立
上恒成立又
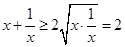 当且仅当
当且仅当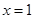 时等号成立.
时等号成立.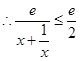
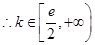
解法二;(I),(II)同解法一
(III)
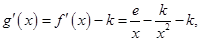
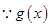
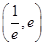 在是减函数,
在是减函数,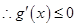 在
在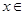
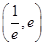 上恒成立
上恒成立即
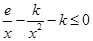 在
在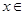
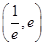 上恒成立
上恒成立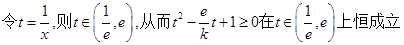
不妨设
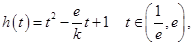
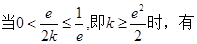
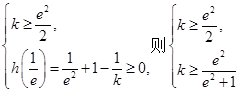
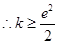
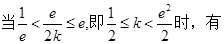
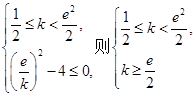
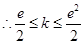
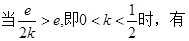
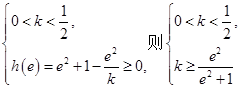
由于
 无解.
无解.综上所述,得出
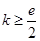 ,即
,即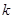 的取值范围是
的取值范围是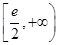

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案
相关题目
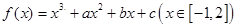 ,且函数
,且函数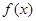 在
在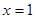 和
和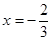 处都取得极值。
处都取得极值。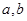 的值;
的值;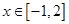 ,
,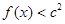 恒成立,求实数
恒成立,求实数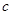 的取值范围。
的取值范围。 (
(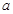 为实常数)。
为实常数)。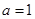 时,求函数
时,求函数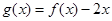 的单调区间;
的单调区间;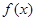 在区间
在区间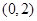 上无极值,求
上无极值,求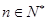 且
且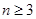 ,求证:
,求证: 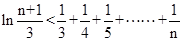 .
.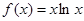 ,
,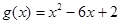 。
。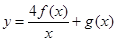 的单调递增区间;
的单调递增区间; 在区间
在区间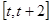
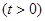 上的最小值;
上的最小值;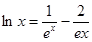 (其中
(其中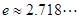 )是否有实数解?并说明理由。
)是否有实数解?并说明理由。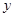 =
=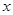 +
+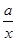 有如下性质:如果常数
有如下性质:如果常数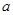 >0,那么该函数在
>0,那么该函数在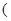 0,
0,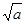
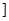 上是减函数,在
上是减函数,在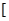
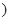 上是增函数.
上是增函数.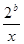 (
(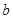 的值;
的值;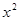 +
+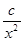 (常数
(常数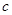 >0)在定义域内的单调性,并说明理由;
>0)在定义域内的单调性,并说明理由;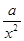 (常数
(常数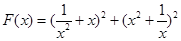 (
(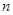 是正整数)在区间[
是正整数)在区间[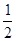 ,2]上的最大值和最小值(可利用你的研究结论).
,2]上的最大值和最小值(可利用你的研究结论).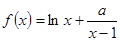 在
在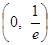 内有极值。
内有极值。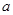 的取值范围;
的取值范围;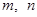 分别为
分别为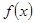 的极大值和极小值,记
的极大值和极小值,记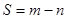 ,求S的取值范围。
,求S的取值范围。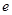 为自然对数的底数)
为自然对数的底数)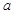 为实数,函数
为实数,函数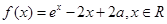
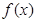 的单调区间
的单调区间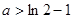 且
且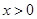 时,有
时,有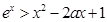
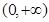 恰有一个零点,求实数
恰有一个零点,求实数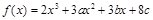 在
在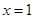 及
及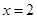 时取得极值.
时取得极值.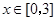 ,都有
,都有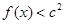 成立,求c的取值范围.
成立,求c的取值范围.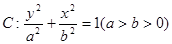 的两焦点与短轴的一个端点连结成等腰直角三角形,直线
的两焦点与短轴的一个端点连结成等腰直角三角形,直线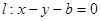 是抛物线
是抛物线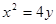 的一条切线。
的一条切线。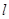 交椭圆
交椭圆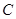 于A、B两点,若点P满足
于A、B两点,若点P满足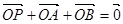 (O为坐标原点), 判断点P是否在椭圆
(O为坐标原点), 判断点P是否在椭圆