题目内容
某工厂生产甲、乙两种产品,计划每天每种产品的生产量不少于15吨,已知生产甲产品1吨,需煤9吨,电力4千瓦时,劳力3个;生产乙产品1吨,需煤4吨,电力5千瓦时,劳力10个;甲产品每吨的利润为7万元,乙产品每吨的利润为12万元;但每天用煤不超过300吨,电力不超过200千瓦时,劳力只有300个.问每天生产甲、乙两种产品各多少吨,才能使利润总额达到最大?分析:先设每天生产甲、乙两种产品分别为x吨、y吨,利润总额为z万元,根据题意抽象出x,y满足的条件,建立约束条件,作出可行域,再根据目标函数z=7x+12y,利用截距模型,平移直线找到最优解,即可.
解答: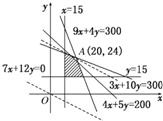 解:设每天生产甲、乙两种产品分别为x吨、y吨,利润总额为z万元,
解:设每天生产甲、乙两种产品分别为x吨、y吨,利润总额为z万元,
则线性约束条件为
目标函数为z=7x+12y,作出可行域如图,
作出一组平行直线7x+12y=t,
当直线经过直线4x+5y=200和直线3x+10y=300的交点A(20,24)时,利润最大.
即生产甲、乙两种产品分别为20吨、24吨时,利润总额最大,zmax=7×20+12×24=428(万元).
 解:设每天生产甲、乙两种产品分别为x吨、y吨,利润总额为z万元,
解:设每天生产甲、乙两种产品分别为x吨、y吨,利润总额为z万元,则线性约束条件为
|
目标函数为z=7x+12y,作出可行域如图,
作出一组平行直线7x+12y=t,
当直线经过直线4x+5y=200和直线3x+10y=300的交点A(20,24)时,利润最大.
即生产甲、乙两种产品分别为20吨、24吨时,利润总额最大,zmax=7×20+12×24=428(万元).
点评:本题主要考查用线性规划解决实际问题中的最值问题,基本思路是抽象约束条件,作出可行域,利用目标函数的类型,找到最优解.属中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 18、某工厂生产甲、乙两种产品,每种产品都是经过第一道和第二道工序加工而成,两道工序的加工结果相互独立,每道工序的加工结果均有A、B两个等级,对每种产品,两道工序的加工结果都为A级时,产品为一等品,其余均为二等品
18、某工厂生产甲、乙两种产品,每种产品都是经过第一道和第二道工序加工而成,两道工序的加工结果相互独立,每道工序的加工结果均有A、B两个等级,对每种产品,两道工序的加工结果都为A级时,产品为一等品,其余均为二等品