题目内容
已知两点A(-2,1),B(4,3),求经过两直线2x-3y+1=0和3x+2y-1=0的交点和线段AB中点的直线l的方程.
l的方程为7x-4y+1=0.
解析:
解法一:由![]() 得
得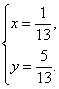
∴交点坐标为![]() .
.
又线段AB中点坐标为(1,2),
∴由两点式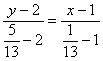 ,
,
得l的方程为7x-4y+1=0.
解法二:设所求直线l的方程为2x-3y+1+λ(3x+2y-1)=0,
整理得(2+3λ)x+(2λ-3)y+(1-λ)=0.
∵直线l过线段AB的中点M(1,2),
∴(2+3λ)×1+(2λ-3)×2+(1-λ)=0.
可得![]() .
.
代入直线方程得l的方程为7x-4y+1=0.

练习册系列答案
相关题目