题目内容
7.已知四边形ABCD是⊙O的内接梯形,AB∥CD,AB=8cm,CD=6cm,⊙O的半径等于5cm,则梯形ABCD的面积为7cm2或49cm2.分析 过点O作OE⊥AB,E为垂足,OF⊥CD,F为垂足,由勾股定理得OE=3,OF=4,当圆心O在梯形ABCD内部时,EF=3+4=7,当圆心O在梯形ABCD外部时,EF=4-3=1,由此能求出梯形ABCD的面积.
解答  解:连接OA,OB,OC,OD,
解:连接OA,OB,OC,OD,
过点O作OE⊥AB,E为垂足,OF⊥CD,F为垂足,
E,O,F三点共线.
等腰三角形OAB中,AE=$\frac{AB}{2}$=4,
由勾股定理得,OE=$\sqrt{{5}^{2}-{4}^{2}}$=3
同理得,OF=$\sqrt{{5}^{2}-{3}^{2}}$=4,
当圆心O在梯形ABCD内部时,
EF=3+4=7,
∴梯形ABCD的面积S=$\frac{6+8}{2}×7$=49(cm2)
当圆心O在梯形ABCD外部时,
EF=4-3=1,
∴梯形ABCD的面积S=$\frac{6+8}{2}×1=7$(cm2).
故答案为:7cm2或49cm2.
点评 本题考查梯形面积的求法,是中档题,解题时要注意勾股定理的合理运用,易错点是容量丢解.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
15.若方程x2+y2-2x-4y+m=0表示圆,则m的取值范围是( )
| A. | m≥5 | B. | m≤5 | C. | m>5 | D. | m<5 |
2.某超市要将甲、乙两种大小不同的袋装大米分装成A,B两种规格的小袋,每袋大米可同时分得A,B两种规格的小袋大米的袋数如下表所示:
已知库房中现有甲、乙两种袋装大米的数量分别为5袋和10袋,市场急需A,B两种规格的成品数分别为15袋和27袋.
(Ⅰ)问分甲、乙两种袋装大米各多少袋可得到所需A,B两种规格的成品数,且使所用的甲、乙两种袋装大米的袋数最少?(要求画出可行域)
(Ⅱ)若在可行域的整点中任意取出一解,求其恰好为最优解的概率.
| 规格类型 袋装大米类型 | A | B |
| 甲 | 2 | 1 |
| 乙 | 1 | 3 |
(Ⅰ)问分甲、乙两种袋装大米各多少袋可得到所需A,B两种规格的成品数,且使所用的甲、乙两种袋装大米的袋数最少?(要求画出可行域)
(Ⅱ)若在可行域的整点中任意取出一解,求其恰好为最优解的概率.
12.已知$\overrightarrow{a},\overrightarrow{b}$是单位向量,它们的夹角为1200,则$\overrightarrow{a}•(\overrightarrow{a}-\overrightarrow{4b})$的值为( )
| A. | 3 | B. | -1 | C. | $1+2\sqrt{3}$ | D. | $1-2\sqrt{3}$ |
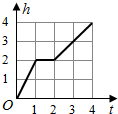
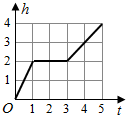
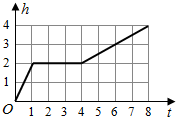
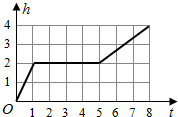
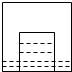 一天,小亮看到家中的塑料桶中有一个竖直放置的玻璃杯,桶子和玻璃杯的形状都是圆柱形,桶口的半径是杯口半径的2倍,其主视图如左图所示.小亮决定做个试验:把塑料桶和玻璃杯看作一个容器,对准杯口匀速注水,注水过程中杯子始终竖直放置,则下列能反映容器最高水位h与注水时间t之间关系的大致图象是( )
一天,小亮看到家中的塑料桶中有一个竖直放置的玻璃杯,桶子和玻璃杯的形状都是圆柱形,桶口的半径是杯口半径的2倍,其主视图如左图所示.小亮决定做个试验:把塑料桶和玻璃杯看作一个容器,对准杯口匀速注水,注水过程中杯子始终竖直放置,则下列能反映容器最高水位h与注水时间t之间关系的大致图象是( )