题目内容
给出下列结论:
①当a<0时,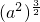 =a3;
=a3;
②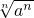 =|a|(n>1,n∈N?,n为偶数);
=|a|(n>1,n∈N?,n为偶数);
③函数f(x)=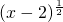 -(3x-7)0的定义域是{x|x≥2且x≠
-(3x-7)0的定义域是{x|x≥2且x≠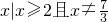 ;
;
④若2x=16,3y= ,则x+y=7.
,则x+y=7.
其中正确的是
- A.①②
- B.②③
- C.③④
- D.②④
B
分析:根据a的取值判定①②的正误,求出定义域判定③,求出x的值判定④,最后确定结果.
解答:∵a<0时,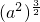 >0,a3<0,∴①错;
>0,a3<0,∴①错;
②显然正确;解 ,得x≥2且x≠
,得x≥2且x≠ ,∴③正确;
,∴③正确;
∵2x=16,∴x=4,∵3y= =3-3,∴y=-3,
=3-3,∴y=-3,
∴x+y=4+(-3)=1,∴④错.故②③正确.
故选B
点评:本题考查有理数指数幂的运算性质,函数的定义域及其求法,是基础题.
分析:根据a的取值判定①②的正误,求出定义域判定③,求出x的值判定④,最后确定结果.
解答:∵a<0时,
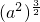 >0,a3<0,∴①错;
>0,a3<0,∴①错;②显然正确;解
 ,得x≥2且x≠
,得x≥2且x≠ ,∴③正确;
,∴③正确;∵2x=16,∴x=4,∵3y=
 =3-3,∴y=-3,
=3-3,∴y=-3,∴x+y=4+(-3)=1,∴④错.故②③正确.
故选B
点评:本题考查有理数指数幂的运算性质,函数的定义域及其求法,是基础题.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目