题目内容
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() :
: ![]() (
(![]() )的离心率
)的离心率![]() 且椭圆
且椭圆![]() 上的点到点
上的点到点![]() 的距离的最大值为3.
的距离的最大值为3.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)在椭圆![]() 上,是否存在点
上,是否存在点![]() ,使得直线
,使得直线![]() :
: ![]() 与圆
与圆![]() :
: ![]() 相交于不同的两点
相交于不同的两点![]() 、
、![]() ,且
,且![]() 的面积最大?若存在,求出点
的面积最大?若存在,求出点![]() 的坐标及对应的
的坐标及对应的![]() 的面积;若不存在,请说明理由.
的面积;若不存在,请说明理由.
【答案】(1)![]() ;(2)存在,M的坐标为
;(2)存在,M的坐标为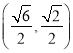 、
、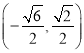 、
、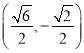 、
、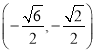 ,最大值为
,最大值为![]() 。
。
【解析】试题分析:(1)离心率![]() ,得到
,得到![]() ,即此时椭圆方程为
,即此时椭圆方程为![]() ,设椭圆上的点为P
,设椭圆上的点为P![]() ,
,
两点间的距离等于3,可得到b=1,所以可求得椭圆方程;(2)在解析几何中,三角形的面积公式通常有两种计算方式,![]()
![]() ,本题由于没有给出角度的关系,所以采用第一种方法。通过联立方程即可得到M的坐标。
,本题由于没有给出角度的关系,所以采用第一种方法。通过联立方程即可得到M的坐标。
试题解析:(Ⅰ)因为![]() ,所以
,所以![]() ,于是
,于是![]() . 1分
. 1分
设椭圆![]() 上任一点
上任一点![]() ,椭圆方程为
,椭圆方程为![]() ,
,![]() ,
,![]()
![]()
![]() =
=
![]()
![]()
①当![]() ,即
,即![]() 时,
时,![]() (此时
(此时![]()
![]() 舍去; 3分
舍去; 3分
②当![]() 即
即![]() 时,
时,![]() 5分
5分
综上椭圆C的方程为![]() 。 6分
。 6分
(Ⅱ)圆心到直线![]() 的距离为
的距离为![]() ,弦长
,弦长![]() ,所以
,所以![]() 的面积为
的面积为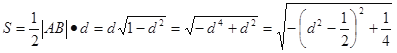 8分
8分
![]() 点
点![]() ,
,![]()
![]() 10分
10分
当![]() 时,
时,![]() 由
由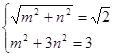 得
得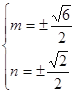
综上所述,椭圆上存在四个点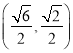 、
、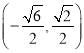 、
、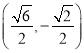 、
、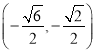 ,使得直线与圆相交于不同的两点
,使得直线与圆相交于不同的两点![]() 、
、![]() ,且
,且![]() 的面积最大,且最大值为
的面积最大,且最大值为![]() . 12分
. 12分

 阅读快车系列答案
阅读快车系列答案【题目】某校数学课外兴趣小组为研究数学成绩是否与性别有关,先统计本校高三年级每个学生一学期数学成绩平均分(采用百分制),剔除平均分在![]() 分以下的学生后,共有男生
分以下的学生后,共有男生![]() 名,女生
名,女生![]() 名.现采用分层抽样的方法,从中抽取了
名.现采用分层抽样的方法,从中抽取了![]() 名学生,按性别分为两组,并将两组学生成绩分为
名学生,按性别分为两组,并将两组学生成绩分为![]() 组,得到如下所示频数分布表.
组,得到如下所示频数分布表.
分数段 |
|
|
|
|
|
|
男 |
|
|
|
|
|
|
女 |
|
|
|
|
|
|
(Ⅰ)规定![]() 分以上为优分(含
分以上为优分(含![]() 分),请你根据已知条件作出
分),请你根据已知条件作出![]() 列联表.
列联表.
优分 | 非优分 | 合计 | |
男生 | |||
女生 | |||
合计 |
|
(Ⅱ)根据你作出的![]() 列联表判断是否有
列联表判断是否有![]() 以上的把握认为“数学成绩与性别有关”.
以上的把握认为“数学成绩与性别有关”.
附表及公式:
|
|
|
|
|
|
|
|
|
|
 ,其中
,其中![]() .
.
【题目】随着电商的快速发展,快递业突飞猛进,到目前,中国拥有世界上最大的快递市场.某快递公司收取快递费用的标准是:重量不超过![]() 的包裹收费10元;重量超过
的包裹收费10元;重量超过![]() 的包裹,除
的包裹,除![]() 收费10元之外,每超过
收费10元之外,每超过![]() (不足
(不足![]() ,按
,按![]() 计算)需再收5元.
计算)需再收5元.
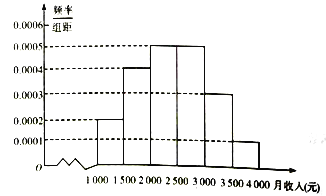
该公司将最近承揽的100件包裹的重量统计如下:
包裹重量(单位: | 1 | 2 | 3 | 4 | 5 |
包裹件数 | 43 | 30 | 15 | 8 | 4 |
公司对近60天,每天揽件数量统计如下表:
包裹件数范围 | 0~100 | 101~200 | 201~300 | 301~400 | 401~500 |
包裹件数(近似处理) | 50 | 150 | 250 | 350 | 450 |
天数 | 6 | 6 | 30 | 12 | 6 |
以上数据已做近似处理,并将频率视为概率.
(1)计算该公司未来5天内恰有2天揽件数在101~300之间的概率;
(2)①估计该公司对每件包裹收取的快递费的平均值;
②根据以往的经验,公司将快递费的三分之一作为前台工作人员的工资和公司利润,剩余的用作其他费用.目前前台有工作人员3人,每人每件揽件不超过150件,日工资100元.公司正在考虑是否将前台工作人员裁减1人,试计算裁员前后公司每日利润的数学期望,若你是公司老总,是否进行裁减工作人员1人?