题目内容
已知以原点O为中心的椭圆的一条准线方程为 ,离心率
,离心率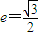 ,M是椭圆上的动点
,M是椭圆上的动点(Ⅰ)若C,D的坐标分别是
 ,求|MC|•|MD|的最大值;
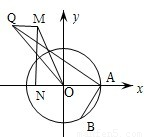
,求|MC|•|MD|的最大值;(Ⅱ)如题(20)图,点A的坐标为(1,0),B是圆x2+y2=1上的点,N是点M在x轴上的射影,点Q满足条件:
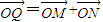 ,
, 、求线段QB的中点P的轨迹方程.
、求线段QB的中点P的轨迹方程.
【答案】分析:(Ⅰ)由题设条件知焦点在y轴上,故设椭圆方程为 (a>b>0).设
(a>b>0).设 ,由准线方程
,由准线方程 .由此能够求出椭圆方程.从而得到点M的坐标为(±1,0)时上式取等号,|MC|•|MD|的最大值为4.
.由此能够求出椭圆方程.从而得到点M的坐标为(±1,0)时上式取等号,|MC|•|MD|的最大值为4.
(II)设M(xm,ym),B(xB,yB)Q(xQ,yQ).因为 ,故xQ=2xN,yQ=yM,xQ2+yQ2=(2xM)2+yy=4.因为
,故xQ=2xN,yQ=yM,xQ2+yQ2=(2xM)2+yy=4.因为 ,(1-xQ-yQ)•(1-xN-yn)=(1-xQ)(1-xN)+yQyN=0,所以xQxN+yQyN=xN+xQ-1.由此可导出动点P的轨迹方程为
,(1-xQ-yQ)•(1-xN-yn)=(1-xQ)(1-xN)+yQyN=0,所以xQxN+yQyN=xN+xQ-1.由此可导出动点P的轨迹方程为 .
.
解答: 解:(Ⅰ)由题设条件知焦点在y轴上,
解:(Ⅰ)由题设条件知焦点在y轴上,
故设椭圆方程为 (a>b>0).
(a>b>0).
设 ,由准线方程
,由准线方程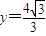 得.
得.
由 得
得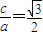 ,解得a=2,c=
,解得a=2,c= ,
,
从而b=1,椭圆方程为 .
.
又易知C,D两点是椭圆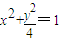 的焦点,
的焦点,
所以,|MC|+|MD|=2a=4
从而|MC|•|MD| ,
,
当且仅当|MC|=|MD|,
即点M的坐标为(±1,0)时上式取等号,|MC|•|MD|的最大值为4.
(II)如图(20)图,设M(xm,ym),B(xB,yB)Q(xQ,yQ).
因为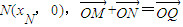 ,
,
故xQ=2xN,yQ=yM,xQ2+yQ2=(2xM)2+yy=4①
因为 ,
,
(1-xQ-yQ)•(1-xN-yn)
=(1-xQ)(1-xN)+yQyN=0,
所以xQxN+yQyN=xN+xQ-1.②
记P点的坐标为(xP,yP),因为P是BQ的中点
所以2xP=xQ+xP,2yP=yQ+yP
由因为xN2+yN2=1,结合①,②得

=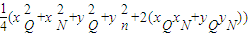
=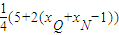 =
=
故动点P的轨迹方程为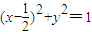
点评:本题考查圆锥曲线的综合应用,解题时要认真审题,仔细求解.
 (a>b>0).设
(a>b>0).设 ,由准线方程
,由准线方程 .由此能够求出椭圆方程.从而得到点M的坐标为(±1,0)时上式取等号,|MC|•|MD|的最大值为4.
.由此能够求出椭圆方程.从而得到点M的坐标为(±1,0)时上式取等号,|MC|•|MD|的最大值为4.(II)设M(xm,ym),B(xB,yB)Q(xQ,yQ).因为
 ,故xQ=2xN,yQ=yM,xQ2+yQ2=(2xM)2+yy=4.因为
,故xQ=2xN,yQ=yM,xQ2+yQ2=(2xM)2+yy=4.因为 ,(1-xQ-yQ)•(1-xN-yn)=(1-xQ)(1-xN)+yQyN=0,所以xQxN+yQyN=xN+xQ-1.由此可导出动点P的轨迹方程为
,(1-xQ-yQ)•(1-xN-yn)=(1-xQ)(1-xN)+yQyN=0,所以xQxN+yQyN=xN+xQ-1.由此可导出动点P的轨迹方程为 .
.解答:
 解:(Ⅰ)由题设条件知焦点在y轴上,
解:(Ⅰ)由题设条件知焦点在y轴上,故设椭圆方程为
 (a>b>0).
(a>b>0).设
 ,由准线方程
,由准线方程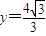 得.
得.由
 得
得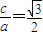 ,解得a=2,c=
,解得a=2,c= ,
,从而b=1,椭圆方程为
 .
.又易知C,D两点是椭圆
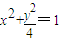 的焦点,
的焦点,所以,|MC|+|MD|=2a=4
从而|MC|•|MD|
 ,
,当且仅当|MC|=|MD|,
即点M的坐标为(±1,0)时上式取等号,|MC|•|MD|的最大值为4.
(II)如图(20)图,设M(xm,ym),B(xB,yB)Q(xQ,yQ).
因为
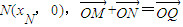 ,
,故xQ=2xN,yQ=yM,xQ2+yQ2=(2xM)2+yy=4①
因为
 ,
,(1-xQ-yQ)•(1-xN-yn)
=(1-xQ)(1-xN)+yQyN=0,
所以xQxN+yQyN=xN+xQ-1.②
记P点的坐标为(xP,yP),因为P是BQ的中点
所以2xP=xQ+xP,2yP=yQ+yP
由因为xN2+yN2=1,结合①,②得

=
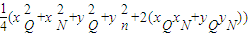
=
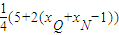 =
=
故动点P的轨迹方程为
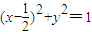
点评:本题考查圆锥曲线的综合应用,解题时要认真审题,仔细求解.

练习册系列答案
相关题目
 已知以原点O为中心的椭圆的一条准线方程为
已知以原点O为中心的椭圆的一条准线方程为 已知以原点O为中心的双曲线的一条准线方程为
已知以原点O为中心的双曲线的一条准线方程为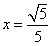 ,离心率e=
,离心率e=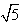 ,
,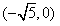 ,B是圆x2+(y-
,B是圆x2+(y-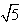 )2=1上的点,点M在双曲线右支上,求|MA|+|MB|的最小值,并求此时M点的坐标。
)2=1上的点,点M在双曲线右支上,求|MA|+|MB|的最小值,并求此时M点的坐标。 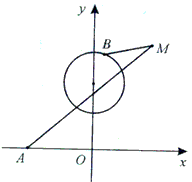
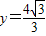 ,离心率
,离心率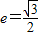 ,M是椭圆上的动点
,M是椭圆上的动点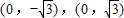 ,求|MC|•|MD|的最大值;
,求|MC|•|MD|的最大值;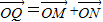 ,
,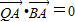 、求线段QB的中点P的轨迹方程.
、求线段QB的中点P的轨迹方程.