题目内容
已知以原点O为中心的双曲线的一条准线方程为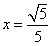 ,离心率e=
,离心率e=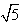 ,
,
(Ⅰ)求该双曲线的方程;
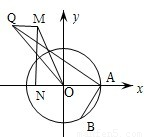
(Ⅱ)如图,点A的坐标为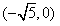 ,B是圆x2+(y-
,B是圆x2+(y-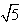 )2=1上的点,点M在双曲线右支上,求|MA|+|MB|的最小值,并求此时M点的坐标。
)2=1上的点,点M在双曲线右支上,求|MA|+|MB|的最小值,并求此时M点的坐标。
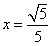 ,离心率e=
,离心率e=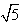 ,
,(Ⅰ)求该双曲线的方程;
(Ⅱ)如图,点A的坐标为
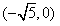 ,B是圆x2+(y-
,B是圆x2+(y-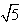 )2=1上的点,点M在双曲线右支上,求|MA|+|MB|的最小值,并求此时M点的坐标。
)2=1上的点,点M在双曲线右支上,求|MA|+|MB|的最小值,并求此时M点的坐标。 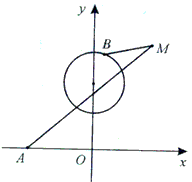
解:(Ⅰ)由题意可知,双曲线的焦点在x轴上,
故可设双曲线的方程为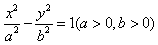 ,
,
设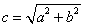 ,
,
由准线方程为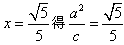 ,
,
由 ,
,
解得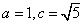 ,从而b=2,
,从而b=2,
∴该双曲线的方程为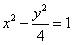 ;
;
(Ⅱ)设点D的坐标为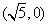 ,
,
则点A、D为双曲线的焦点,|MA|-|MD|=2a=2,
所以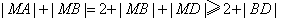 ,
,
∵B是圆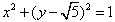 上的点,其圆心为
上的点,其圆心为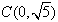 ,半径为1,
,半径为1,
故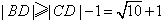 ,
,
从而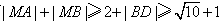 ,
,
当M,B在线段CD上时取等号,此时|MA|+|MB|的最小值为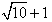 ;
;
∵直线CD的方程为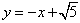 ,
,
因点M在双曲线右支上,故x>0,
由方程组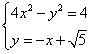 ,解得
,解得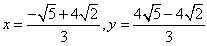 ,
,
所以M点的坐标为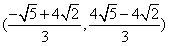 。
。
故可设双曲线的方程为
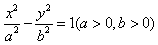 ,
,设
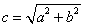 ,
,由准线方程为
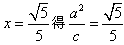 ,
,由
 ,
,解得
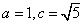 ,从而b=2,
,从而b=2,∴该双曲线的方程为
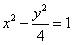 ;
;(Ⅱ)设点D的坐标为
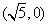 ,
,则点A、D为双曲线的焦点,|MA|-|MD|=2a=2,
所以
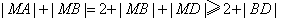 ,
, ∵B是圆
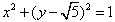 上的点,其圆心为
上的点,其圆心为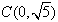 ,半径为1,
,半径为1,故
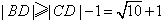 ,
,从而
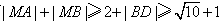 ,
,当M,B在线段CD上时取等号,此时|MA|+|MB|的最小值为
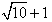 ;
;∵直线CD的方程为
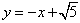 ,
,因点M在双曲线右支上,故x>0,
由方程组
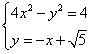 ,解得
,解得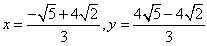 ,
,所以M点的坐标为
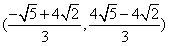 。
。 
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 已知以原点O为中心的椭圆的一条准线方程为
已知以原点O为中心的椭圆的一条准线方程为 已知以原点O为中心的双曲线的一条准线方程为
已知以原点O为中心的双曲线的一条准线方程为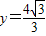 ,离心率
,离心率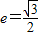 ,M是椭圆上的动点
,M是椭圆上的动点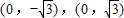 ,求|MC|•|MD|的最大值;
,求|MC|•|MD|的最大值;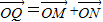 ,
,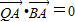 、求线段QB的中点P的轨迹方程.
、求线段QB的中点P的轨迹方程.