题目内容
 。
。
(Ⅰ)求 的极值点;
的极值点;
(Ⅱ)当 时,若方程
时,若方程 在
在 上有两个实数解,求实数t的取值范围;
上有两个实数解,求实数t的取值范围;
(Ⅲ)证明:当 时,
时, 。
。
(Ⅰ)①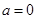 时,
时,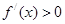 , ∴
, ∴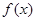 在(-1,+∞)上是增函数,函数既无极大值点,也无极小值点;②当
在(-1,+∞)上是增函数,函数既无极大值点,也无极小值点;②当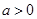 时,
时,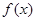 在
在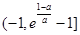 上递增,在
上递增,在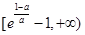 单调递减,函数的极大值点为
单调递减,函数的极大值点为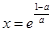 -1,无极小值点;③当
-1,无极小值点;③当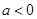 时,
时,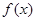 在
在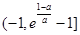 上递减,在
上递减,在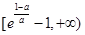 单调递增,函数的极小值点为
单调递增,函数的极小值点为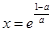 -1,无极大值点;(Ⅱ)当
-1,无极大值点;(Ⅱ)当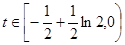 时,方程
时,方程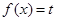 有两解;(Ⅲ)详见解析.
有两解;(Ⅲ)详见解析.
解析试题分析:(Ⅰ)求 的极值点,先求函数的定义域为
的极值点,先求函数的定义域为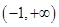 ,然后可对函数
,然后可对函数 求导数得
求导数得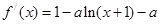 ,令导数等零,求出
,令导数等零,求出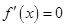 的解,再利用导数大于0,导数小于0,判断函数的单调区间,从而确定极值点,但本题由于含有参数
的解,再利用导数大于0,导数小于0,判断函数的单调区间,从而确定极值点,但本题由于含有参数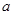 ,需对
,需对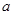 讨论(Ⅱ)当
讨论(Ⅱ)当 时,若方程
时,若方程 在
在 上有两个实数解,求实数t的取值范围,由(Ⅰ)知,
上有两个实数解,求实数t的取值范围,由(Ⅰ)知, 在
在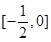 上单调递增,在
上单调递增,在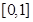 上单调递减,而
上单调递减,而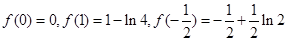 ,由此可得实数t的取值范围;(Ⅲ)根据要证明当
,由此可得实数t的取值范围;(Ⅲ)根据要证明当 时,
时, ,直接证明比较困难,可以利用分析法来证明本题,从结论入手,要证结论只要证明后面这个式子成立,两边取对数,构造函数,问题转化为只要证明函数在一个范围上成立,利用导数证明函数的性质.
,直接证明比较困难,可以利用分析法来证明本题,从结论入手,要证结论只要证明后面这个式子成立,两边取对数,构造函数,问题转化为只要证明函数在一个范围上成立,利用导数证明函数的性质.
试题解析:(Ⅰ)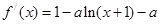 (1分)
(1分)
①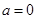 时,
时,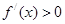 , ∴
, ∴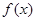 在(-1,+∞)上是增函数,函数既无极大值点,也无极小值点。(2分)
在(-1,+∞)上是增函数,函数既无极大值点,也无极小值点。(2分)
②当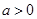 时,
时,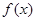 在
在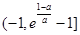 上递增,在
上递增,在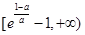 单调递减,函数的极大值点为
单调递减,函数的极大值点为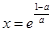 -1,无极小值点(3分)
-1,无极小值点(3分)
③当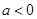 时,
时,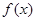 在
在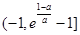 上递减,在
上递减,在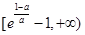 单调递增,函数的极小值点为
单调递增,函数的极小值点为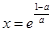 -1,无极大值点(4分)
-1,无极大值点(4分)
(Ⅱ)由(Ⅰ)知,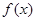 在
在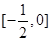 上单调递增,在
上单调递增,在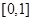 上单调递减,
上单调递减,
又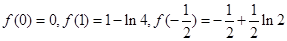 ,
,
∴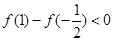 ,∴当
,∴当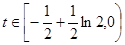 时,方程
时,方程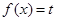 有两解 (8分)
有两解 (8分)
(Ⅲ)要证: 只须证
只须证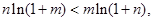
只须证: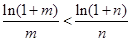 ,
,
设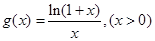
则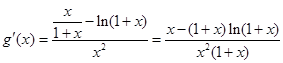 ,(10分)
,(10分)
由(1)知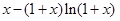 在
在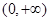 单调递减,(12分)
单调递减,(12分)
∴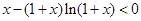 ,即
,即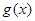 是减函数,而m>n,
是减函数,而m>n,
∴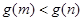 ,故原不等式成立。 (14分)
,故原不等式成立。 (14分)
考点:不等式的证明;利用导数研究函数的单调性.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
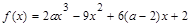 ,
,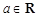 .
.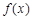 在
在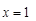 处取得极值,求实数
处取得极值,求实数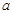 的值;
的值;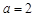 ,求函数
,求函数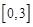 上的最大值和最小值.
上的最大值和最小值.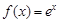 ,
,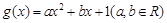 .
.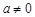 ,则
,则 ,
,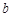 满足什么条件时,曲线
满足什么条件时,曲线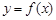 与
与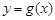 在
在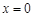 处总有相同的切线?
处总有相同的切线?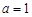 时,求函数
时,求函数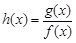 的单调减区间;
的单调减区间;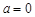 时,若
时,若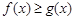 对任意的
对任意的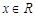 恒成立,求
恒成立,求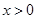 ,函数
,函数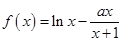 .
.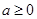 时,讨论函数
时,讨论函数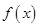 的单调性;
的单调性;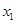 和
和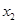 )时,求证:
)时,求证: .
.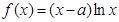 ,
,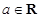 .
.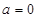 时,求函数
时,求函数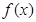 的极小值;
的极小值;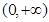 上为增函数,求
上为增函数,求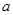 的取值范围.
的取值范围.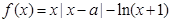 .
. 时,求函数
时,求函数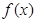 的单调区间;
的单调区间;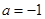 时,若
时,若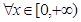 ,
,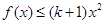 恒成立,求实数
恒成立,求实数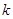 的最小值;
的最小值;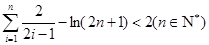 .
.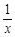 -(2+a)lnx(a≥0)
-(2+a)lnx(a≥0) 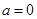 时,求
时,求 的极值;
的极值;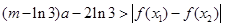 成立,求实数m的取值范围。
成立,求实数m的取值范围。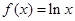 ,
,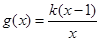 .
.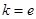 时,求函数
时,求函数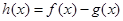 的单调区间和极值;
的单调区间和极值;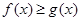 恒成立,求实数
恒成立,求实数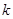 的值.
的值.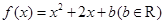 .
.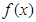 的值域为
的值域为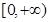 ,若关于
,若关于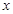 的不等式
的不等式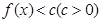 的解集为
的解集为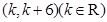 ,求
,求 的值;
的值;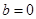 时,
时,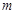 为常数,且
为常数,且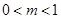 ,
,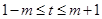 ,求
,求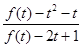 的取值范围.
的取值范围.