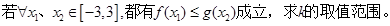题目内容
设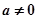 ,函数
,函数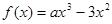 .
.
(1)若函数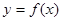 在
在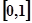 的最小值为-2,求a的值;
的最小值为-2,求a的值;
(2)若函数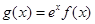 在
在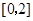 上是单调减函数,求实数
上是单调减函数,求实数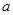 的取值范围.
的取值范围.
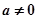 ,函数
,函数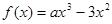 .
.(1)若函数
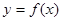 在
在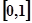 的最小值为-2,求a的值;
的最小值为-2,求a的值;(2)若函数
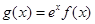 在
在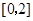 上是单调减函数,求实数
上是单调减函数,求实数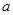 的取值范围.
的取值范围.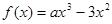 的导函数为
的导函数为 ,
,当
 时,
时, 在
在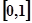 恒成立,所以在
恒成立,所以在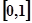 为减函数,最小值为
为减函数,最小值为 ,舍去
,舍去当
 时,
时, ,
,当
 时,
时, 在
在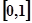 恒成立,所以在
恒成立,所以在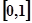 为减函数,最小值为
为减函数,最小值为 ,舍去
,舍去当
 时,在
时,在 为减函数,在
为减函数,在 为增函数,,所以最小值为
为增函数,,所以最小值为
 ,
,(2)
 ,
,
在
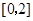 上恒成立,即
上恒成立,即 在
在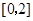 上恒成立,当x=0时成立,当
上恒成立,当x=0时成立,当 时,
时, 恒成立,
恒成立,
 ,
, ,
, 在
在 时为增函数,所以
时为增函数,所以 ,
, ,
,
(1)讨论a的取值,判断函数的自变量x取何值时,取最小值-2;
(2)函数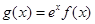 在
在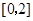 上是单调减函数,转化为导函数在
上是单调减函数,转化为导函数在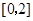 为非负值恒
为非负值恒
成立。
(2)函数
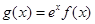 在
在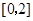 上是单调减函数,转化为导函数在
上是单调减函数,转化为导函数在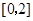 为非负值恒
为非负值恒成立。

练习册系列答案
相关题目
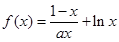
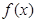 在
在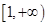 上为增函数,求正实数
上为增函数,求正实数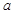 的取值范围;
的取值范围;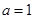 时,求
时,求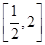 上的最大值和最小值;
上的最大值和最小值;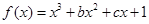 有两个极值点
有两个极值点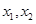 且
且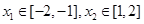 ,则
,则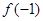 的取值范围是( )
的取值范围是( )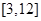
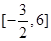
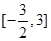
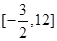
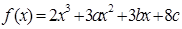 在
在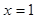 及
及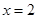 时取得极值.
时取得极值.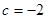 时,求函数
时,求函数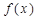 在区间
在区间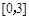 上的最大值.
上的最大值.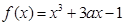 ,
,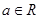 .
. (Ⅰ)若函数
(Ⅰ)若函数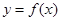 的图象在
的图象在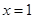 处的切线与直线
处的切线与直线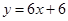 平行,求实数
平行,求实数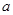 的值;
的值;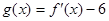 ,对满足
,对满足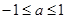 的一切
的一切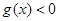 成立,求实数
成立,求实数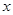 的取值范围;
的取值范围;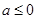 时,请问:是否存在整数
时,请问:是否存在整数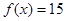 有且只有一个实根?若存在,求出整数
有且只有一个实根?若存在,求出整数 的图像如左图所示,那么函数
的图像如左图所示,那么函数 的图像最有可能的是( )
的图像最有可能的是( )
 的图像过坐标原点
的图像过坐标原点 ,且在点
,且在点 处的切线的斜率是
处的切线的斜率是 .
. ,
, 的值
的值 在区间
在区间 上的值域
上的值域 .
. 极值;
极值;