题目内容
18.已知非零向量$\overrightarrow{a}$,$\overrightarrow{b}$,OA=$\overrightarrow{a}$,OB=$\overrightarrow{b}$,OC=3$\overrightarrow{a}$-2$\overrightarrow{b}$,求证:A,B,C三点在同一条直线上.分析 用$\overrightarrow{a}$,$\overrightarrow{b}$表示出$\overrightarrow{AB}$,$\overrightarrow{AC}$,证明$\overrightarrow{AB}$,$\overrightarrow{AC}$共线即可.
解答 证明:$\overrightarrow{AB}$=$\overrightarrow{OB}$-$\overrightarrow{OA}$=$\overrightarrow{b}-\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{OC}$-$\overrightarrow{OA}$=2$\overrightarrow{a}$-2$\overrightarrow{b}$,
∴$\overrightarrow{AC}$=-2$\overrightarrow{AB}$,
∴A,B,C三点在同一条直线上.
点评 本题考查了平面向量的共线定理,是基础题.

练习册系列答案
相关题目
3.已知平面向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为120°,|$\overrightarrow{b}$|=1,|2$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{13}$,则|$\overrightarrow{a}$-$\overrightarrow{b}$|=( )
| A. | $\sqrt{3}$ | B. | $\sqrt{7}$ | C. | 7 | D. | 3 |
10.下列不等式在给定区间上不恒成立的是( )
| A. | (x+1)cosx<1,x∈(0,π) | B. | e${\;}^{{x}^{2}}$>1+x2,x∈(0,+∞) | ||
| C. | sinx+tanx>2x,x∈(0,$\frac{π}{2}$) | D. | lnx+ex>x$-\frac{1}{x}$+2,x∈(0,+∞) |
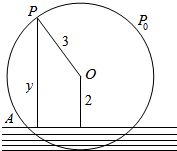 如图为一半径是3米的水轮,水轮圆心O距离水面2米,开始旋转时水轮上的点P在P0位置,P0距离水面3米,已知水轮每分钟旋转4圈,求点P到水面的距离y(米)与时间x(秒)的函数关系式.
如图为一半径是3米的水轮,水轮圆心O距离水面2米,开始旋转时水轮上的点P在P0位置,P0距离水面3米,已知水轮每分钟旋转4圈,求点P到水面的距离y(米)与时间x(秒)的函数关系式.