题目内容
设数列{an}的前n项和为Sn,且Sn=2an-2n+1数列{bn}满足bn=log2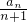 ,其中n∈N*.
,其中n∈N*.
(I)求数列{an}通项公式;
(II)求使不等式(1+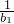 )•(1+
)•(1+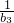 )…(1+
)…(1+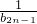 )≥m•
)≥m•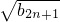 对任意正整数n都成立的最大实数m的值;
对任意正整数n都成立的最大实数m的值;
(III)当n∈N*时,求证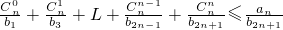 .
.
(Ⅰ)解:由Sn=2an-2n+1,得Sn-1=2an-1-2n(n≥2).
两式相减,得an=2an-2an-1-2n,即an-2an-1=2n(n≥2).
于是 -
-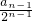 =1,所以数列{
=1,所以数列{ }是公差为1的等差数列.
}是公差为1的等差数列.
又S1=a1=2a1-22,所以a1=4.
所以 =2+(n-1)=n+1,故an=(n+1)•2n
=2+(n-1)=n+1,故an=(n+1)•2n
(II)∵bn=log2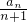 =log22n=n
=log22n=n
∴(1+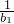 )•(1+
)•(1+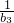 )…(1+
)…(1+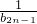 )≥m•
)≥m•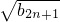 即为(1+1)•(1+
即为(1+1)•(1+ )…(1+
)…(1+ )≥m•
)≥m•
∴m≤ 对任意正整数n都成立
对任意正整数n都成立
令f(n)= ,则f(n+1)=
,则f(n+1)=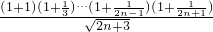
∴ =
= >1
>1
∴f(n)单调递增,故f(n)≥f(1)=
∴m≤
∴m的最大值为 ;
;
(III)证明:欲证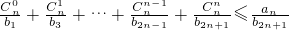
只要证
∵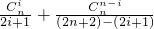 =
=
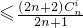
∴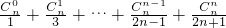 =
= [(
[(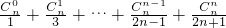 )+(
)+(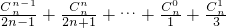 )]
)] =
=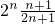
∴ .
.
分析:(Ⅰ)根据数列递推式,确定数列是数列{ }是公差为1的等差数列,将a1=4代入便可求出数列{an}的通项公式;
}是公差为1的等差数列,将a1=4代入便可求出数列{an}的通项公式;
(II)问题可转化为m≤ 对任意正整数n都成立,求出右边函数的最大值,即可求得m的最大值;
对任意正整数n都成立,求出右边函数的最大值,即可求得m的最大值;
(III)欲证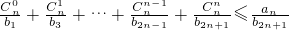 ,只要证
,只要证 ,利用
,利用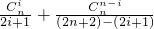 =
=
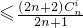 ,即可证得结论.
,即可证得结论.
点评:本题数列递推式,考查数列的通项,考查恒成立问题,考查不等式的证明,正确分离参数是关键.
两式相减,得an=2an-2an-1-2n,即an-2an-1=2n(n≥2).
于是
 -
-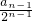 =1,所以数列{
=1,所以数列{ }是公差为1的等差数列.
}是公差为1的等差数列.又S1=a1=2a1-22,所以a1=4.
所以
 =2+(n-1)=n+1,故an=(n+1)•2n
=2+(n-1)=n+1,故an=(n+1)•2n(II)∵bn=log2
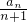 =log22n=n
=log22n=n∴(1+
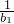 )•(1+
)•(1+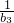 )…(1+
)…(1+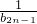 )≥m•
)≥m•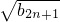 即为(1+1)•(1+
即为(1+1)•(1+ )…(1+
)…(1+ )≥m•
)≥m•
∴m≤
 对任意正整数n都成立
对任意正整数n都成立令f(n)=
 ,则f(n+1)=
,则f(n+1)=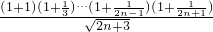
∴
 =
= >1
>1∴f(n)单调递增,故f(n)≥f(1)=

∴m≤

∴m的最大值为
 ;
;(III)证明:欲证
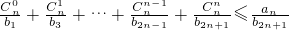
只要证

∵
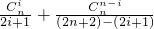 =
=
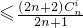
∴
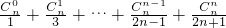 =
= [(
[(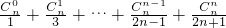 )+(
)+(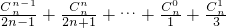 )]
)] =
=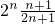
∴
 .
.分析:(Ⅰ)根据数列递推式,确定数列是数列{
 }是公差为1的等差数列,将a1=4代入便可求出数列{an}的通项公式;
}是公差为1的等差数列,将a1=4代入便可求出数列{an}的通项公式;(II)问题可转化为m≤
 对任意正整数n都成立,求出右边函数的最大值,即可求得m的最大值;
对任意正整数n都成立,求出右边函数的最大值,即可求得m的最大值;(III)欲证
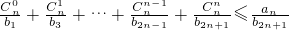 ,只要证
,只要证 ,利用
,利用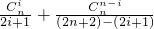 =
=
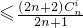 ,即可证得结论.
,即可证得结论.点评:本题数列递推式,考查数列的通项,考查恒成立问题,考查不等式的证明,正确分离参数是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目