题目内容
【题目】已知数列![]() 的各项排成如图所示的三角形数阵,数阵中每一行的第一个数
的各项排成如图所示的三角形数阵,数阵中每一行的第一个数![]() 构成等差数列
构成等差数列![]() ,
,![]() 是
是![]() 的前
的前![]() 项和,且
项和,且![]() ,
,![]() .
.
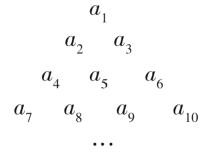
(1)若数阵中从第3行开始每行中的数按从左到右的顺序均构成公比为正数的等比数列,且公比相等,已知![]() ,求
,求![]() 的值;
的值;
(2)设![]() ,当
,当![]() 时,对任意
时,对任意![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)160;(2)![]() 或
或![]() .
.
【解析】
试题(I)由等差数列{bn}满足b1=a1=1,S5=15.求出数列的公差后,可得数列的通项公式,结合数阵中从第三行开始每行中的数按从左到右的顺序均构成公比为正数的等比数列,且公比相等,a9=16,可求出公比,进而求出a50的值;
(Ⅱ)由(1)求出Sn的表达式,利用裂项相消法求出Tn的表达式,进而将不等式恒成立问题,转化为最值问题,利用导数法,可得答案.
试题解析:
(1)设等差数列![]() 的公差为
的公差为![]() ,∵
,∵![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
∴![]() ,
,
设从第3行起,每行的公比都是![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() ,故
,故![]() 是数阵中第10行的第5个数.
是数阵中第10行的第5个数.
故![]() .
.
(2)∵![]() ,
,
∴![]()
![]()
![]()
![]() ;
;
令![]() ,
,
则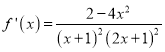
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上为减函数,
上为减函数,
∴![]() 为递减数列,
为递减数列,![]() 的最大值为
的最大值为![]() .
.
∴不等式变为![]() 恒成立,设
恒成立,设![]() ,
,![]() ,
,
则 ,即
,即 ,解得
,解得![]() 或
或![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】对甲、乙两名自行车赛手在相同条件下进行了6次测试,测得他们的最大速度(单位:m/s)的数据如下:
甲 | 27 | 38 | 30 | 37 | 35 | 31 |
乙 | 33 | 29 | 38 | 34 | 28 | 36 |
(1)画出茎叶图,由茎叶图你能获得哪些信息?
(2)分别求出甲、乙两名自行车赛手最大速度(m/s)数据的平均数、极差、方差,并判断选谁参加比赛比较合适?
【题目】微信是现代生活中进行信息交流的重要工具.据统计,某公司200名员工中![]() 的人使用微信,其中每天使用微信时间少于一小时的有60人,其余的员工每天使用微信时间不少于一小时,若将员工分成青年(年龄小于40岁)和中年(年龄不小于40岁)两个阶段,那么使用微信的人中
的人使用微信,其中每天使用微信时间少于一小时的有60人,其余的员工每天使用微信时间不少于一小时,若将员工分成青年(年龄小于40岁)和中年(年龄不小于40岁)两个阶段,那么使用微信的人中![]() 是青年人.若规定:每天使用微信时间不少于一小时为经常使用微信,那么经常使用微信的员工中
是青年人.若规定:每天使用微信时间不少于一小时为经常使用微信,那么经常使用微信的员工中![]() 都是青年人.
都是青年人.
(1)若要调查该公司使用微信的员工经常使用微信与年龄的关系,完成![]() 列联表:
列联表:
青年人 | 中年人 | 合计 | |
经常使用微信 | |||
不经常使用微信 | |||
合计 |
(2)由列联表中所得数据判断,能否在犯错误的概率不超过![]() 的前提下认为“经常使用微信与年龄有关”?
的前提下认为“经常使用微信与年龄有关”?
| 0.010 | 0.001 |
| 6.635 | 10.828 |
![]()