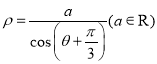题目内容
【题目】已知P(![]() ,1),Q(cosx,sinx),O为坐标原点,函数f(x)
,1),Q(cosx,sinx),O为坐标原点,函数f(x)![]() .
.
(1)求f(x)的解析式及最小正周期;
(2)若A为△ABC的内角,f(A)=4,BC=3,△ABC的面积为![]() ,求AB+AC.
,求AB+AC.
【答案】(1)f(x)=4﹣2sin(x![]() ),T
),T![]() 2π.(2)AB+AC=2
2π.(2)AB+AC=2![]() .
.
【解析】
(1)利用向量数量积的坐标运算,求得![]() 的解析式,进而求得
的解析式,进而求得![]() 的最小正周期.
的最小正周期.
(2)利用![]() ,求得
,求得![]() ,利用三角形的面积公式以及余弦定理,求得
,利用三角形的面积公式以及余弦定理,求得![]() 的值,也即求得
的值,也即求得![]() 的值.
的值.
(1)P(![]() ,1),Q(cosx,sinx),O为坐标原点,
,1),Q(cosx,sinx),O为坐标原点,![]() (
(![]() cosx,1﹣sinx)
cosx,1﹣sinx)
函数f(x)![]() 3
3![]() cosx+1﹣sinx=4﹣2sin(x
cosx+1﹣sinx=4﹣2sin(x![]() ),
),
所以函数的最小正周期为:T![]() 2π.
2π.
(2)若A为△ABC的内角,f(A)=4,4﹣2sin(A![]() )=4,可得A
)=4,可得A![]() ,
,
△ABC的面积为![]() ,
,
BC=3,a2=b2+c2﹣2bccosA=(b+c)2﹣bc=9,可得b+c=2![]() ,
,
即AB+AC=2![]() .
.

练习册系列答案
相关题目