题目内容
(本题满分16分)对于数列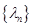 ,若存在常数M>0,对任意
,若存在常数M>0,对任意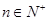 ,恒有
,恒有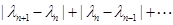
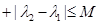 ,则称数列
,则称数列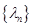 为
为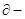 数列.
数列.
求证:⑴设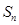 是数列
是数列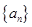 的前n项和,若
的前n项和,若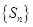 是
是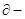 数列,则
数列,则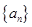 也是
也是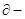 数列.
数列.
⑵若数列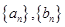 都是
都是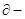 数列,则
数列,则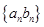 也是
也是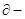 数列.
数列.
【答案】
证明:(1)∵{Sn}为 数列,∴存在M>0, 使
数列,∴存在M>0, 使
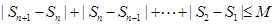
∴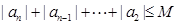 ,又
,又
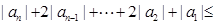
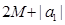 . ∴{an}也是
. ∴{an}也是 数列.
数列.
(2) ∵数列{an}{bn}都是 数列,∴存在M, M'使得:
数列,∴存在M, M'使得:
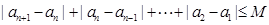 ,
,
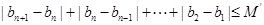 对任意
对任意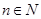 都成立.
都成立.
考虑
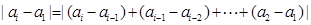

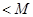 ∴
∴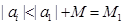
同理,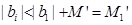
∴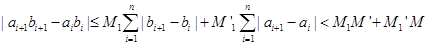
∴{anbn}也是 数列.
数列.
【解析】略

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
 ):
):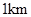 的正方形
的正方形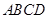 地段进行市场开发,拟在该地段的一角建设一个景观,需要建一条道路
地段进行市场开发,拟在该地段的一角建设一个景观,需要建一条道路 (点
(点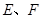 分别在
分别在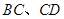 上),根据规划要求
上),根据规划要求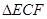 的周长为
的周长为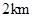 .
.
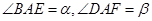 ,求证:
,求证: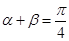 ;
;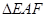 的面积最小,试确定点
的面积最小,试确定点 ,数列
,数列 满足
满足 ,
, ,
, ,
, ,
, 的值;
的值; 是等差数列;
是等差数列; 满足
满足 ,
, ,
,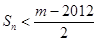 对一切
对一切 成立,求最小正整数
成立,求最小正整数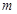 的值.
的值.