题目内容
(本题满分16分)本题共有3个小题,第1小题满分3分,第2小题满分6分,第3小
题满分7分.
已知函数 ,数列
,数列 满足
满足 ,
, ,
,
(1). 求 ,
, ,
, 的值;
的值;
(2). 求证:数列 是等差数列;
是等差数列;
(3). 设数列 满足
满足 ,
, ,
,
若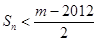 对一切
对一切 成立,求最小正整数
成立,求最小正整数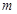 的值.
的值.
【答案】
(1)【解】由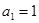 ,
,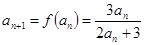 得
得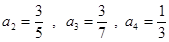 ……3分
……3分
(2)【解】由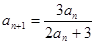 得
得 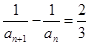 ……8分
……8分
所以,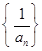 是首项为1,公差为
是首项为1,公差为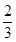 的等差数列
……9分
的等差数列
……9分
(3)【解】由(2)得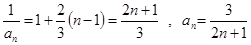 ……-10分
……-10分
当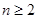 时 ,
时 ,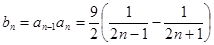 ,当
,当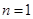 时,上式同样成立, ……12分
时,上式同样成立, ……12分
所以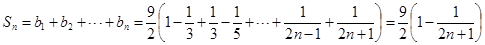
因为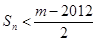 ,所以
,所以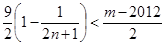 对一切
对一切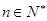 成立, ……14分
成立, ……14分
又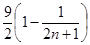 随
随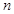 递增,且
递增,且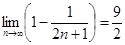 ,所以
,所以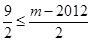 ,
,
所以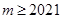 ,
,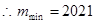 ……16分
……16分
【解析】略

练习册系列答案
相关题目
 为偶函数, 且
为偶函数, 且
 的值;
的值; 为三角形
为三角形 的一个内角,求满足
的一个内角,求满足 的
的 为偶函数, 且
为偶函数, 且
 的值;
的值; 为三角形
为三角形 的一个内角,求满足
的一个内角,求满足 的
的