题目内容
已知f(x)是R上的奇函数,且当x∈(-∞,0)时,f(x)=-xlg(2-x),求f(x)的解析式.
f(x)="-xlg(2+|x|)" (x∈R)
∵f(x)是奇函数,可得f(0)=-f(0),∴f(0)=0.
当x>0时,-x<0,由已知f(-x)=xlg(2+x),∴-f(x)=xlg(2+x),
即f(x)=-xlg(2+x) (x>0).∴f(x)=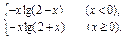
即f(x)="-xlg(2+|x|)" (x∈R).
当x>0时,-x<0,由已知f(-x)=xlg(2+x),∴-f(x)=xlg(2+x),
即f(x)=-xlg(2+x) (x>0).∴f(x)=
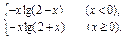
即f(x)="-xlg(2+|x|)" (x∈R).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
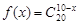 ,集合
,集合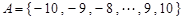 ,判断
,判断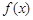 在
在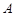 上的奇偶性为( )
上的奇偶性为( )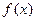 是偶函数,
是偶函数,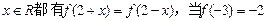 时,
时,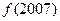 的值为 ( )
的值为 ( )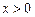 时,
时,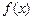 的解析式;
的解析式;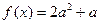 有三个不同的解,求a的取值范围。
有三个不同的解,求a的取值范围。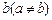 ,当
,当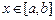 时,
时,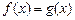 ,且
,且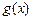 的值域为
的值域为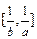 .若存在,求出a、b 的值;若不存在,说明理由
.若存在,求出a、b 的值;若不存在,说明理由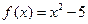 的一个正零点(误差不超过
的一个正零点(误差不超过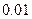 ).
).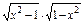 ;
;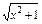 ) (x∈R);
) (x∈R);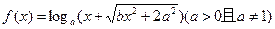 是奇函数,则实数对
是奇函数,则实数对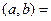 _______
_______ 是
是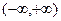 上的奇函数,
上的奇函数,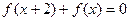 ,当
,当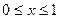 时,
时,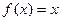 ,则
,则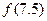 为
为  是定义在[-1,1]上的偶函数,
是定义在[-1,1]上的偶函数, 的图象与
的图象与 对称,且当x∈[ 2,3 ] 时,
对称,且当x∈[ 2,3 ] 时, 222233.(1)求
222233.(1)求 上为增函数,求
上为增函数,求 的取值范围;(3)是否存在正整数
的取值范围;(3)是否存在正整数 上?若存在,求出
上?若存在,求出