Question

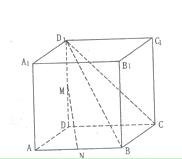
(理)如图4,在体积为1的直三棱柱ABC—A₁B₁C₁中,∠ACB=90°,AC=BC=1.求直线A₁B与平面BB₁C₁C所成角的大小(结果用反三角函数值表示).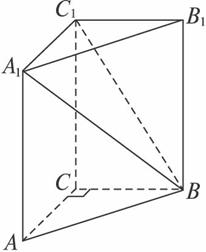

图4

(文)如图5,在正四棱锥P—ABCD中,PA=2,直线PA与平面ABCD所成的角为60°,求正四棱锥P—ABCD的体积V.

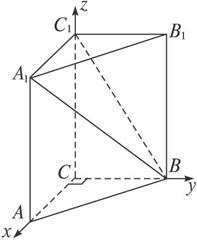
图5

Answer 1

答案：(理)解法一:由题意,可得体积V=CC₁·S_△ABC=CC₁··AC·BC=CC₁=1,

∴AA₁=CC₁=2.

连结BC₁.∵A₁C₁⊥B₁C₁,A₁C₁⊥CC₁,∴A₁C₁⊥平面BB₁C₁C.

∴∠A₁BC₁是直线A₁B与平面BB₁C₁C所成的角.

BC₁=,

∴tan∠A₁BC₁=,则∠A₁BC₁=arctan.

故直线A₁B与平面BB₁C₁C所成角的大小为arctan.

解法二:由题意,可得体积V=CC₁·S_△ABC=CC₁··AC·BC=CC₁=1,∴CC₁=2.

如图,建立空间直角坐标系,得点B(0,1,0),C₁(0,0,2),A₁(1,0,2),

则=(-1,1,-2),平面BB₁C₁C的法向量为n=(1,0,0).

设直线A₁B与平面BB₁C₁C所成的角为θ,与n的夹角为φ,

则cosφ==-,

∴sinθ=|cosφ|=,θ=arcsin.

故直线A₁B与平面BB₁C₁C所成角的大小为arcsin.

(文)解:作PO⊥平面ABCD,垂足为O.连结AO,O是正方形ABCD的中心,∠PAO是直线PA与平面ABCD所成的角.

∠PAO=60°,PA=2,∴PO=,AO=1,AB=.∴V=PO·S_ABCD=××2=.