题目内容
下列命题是真命题的是（ ）
分析：分别根据棱锥，棱柱，棱台的定义分别进行判断即可．
解答：解：A．根据正三棱锥的定义可知，满足侧面是全等的等腰三角形，底面是正三角形的三棱锥是正三棱锥，正确．
B．有两个面互相平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行，由这些面所围成的几何体叫做棱柱棱柱，所以B错误．
C．棱台是由棱锥截来的，故要求等腰梯形的腰延长后要交与一点，所以根据棱台的定义可知，C不正确．
D．根据正棱锥的定义可知，定点在底面的射影必须是底面的中心，所以D不正确．
故选A．
B．有两个面互相平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行，由这些面所围成的几何体叫做棱柱棱柱，所以B错误．
C．棱台是由棱锥截来的，故要求等腰梯形的腰延长后要交与一点，所以根据棱台的定义可知，C不正确．
D．根据正棱锥的定义可知，定点在底面的射影必须是底面的中心，所以D不正确．
故选A．
点评：本题主要考查空间几何体的概念，要求熟练掌握棱锥，棱柱，棱台以及正棱锥的定义．
练习册系列答案
阅读快车系列答案
相关题目
，对
都有
，则
为偶函数
，若对
，都有
，则函数
中心对称
与
是奇函数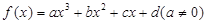
的图形一定是对称中心在图像上的中心对称图形。
有两不同极值点
，若
，且
，则关于的方程
的不同实根个数必有三个.