题目内容
下列命题是真命题的是
①“x=2”是“x2-5x+6=0”的充分不必要条件
②若a>b则ac>bc
③命题“若m>0,则方程x2+x-m=0有实根”的逆否命题为“若方程x2+x-m=0无实根,则m≤0”
④曲线
+
=1是椭圆的充要条件是-4<k<8.
①③
①③
.①“x=2”是“x2-5x+6=0”的充分不必要条件
②若a>b则ac>bc
③命题“若m>0,则方程x2+x-m=0有实根”的逆否命题为“若方程x2+x-m=0无实根,则m≤0”
④曲线
| x2 |
| 8-k |
| y2 |
| k+4 |
分析:①由“x=2”⇒“x2-5x+6=0”,“x2-5x+6=0”⇒“x=2,或x=3”,知“x=2”是“x2-5x+6=0”的充分不必要条件;
②若a>b,c≤0,则ac≤bc;
③命题“若m>0,则方程x2+x-m=0有实根”的逆否命题为“若方程x2+x-m=0无实根,则m≤0”;
④由曲线
+
=1是椭圆,得-4<k<2,或2<k<8.
②若a>b,c≤0,则ac≤bc;
③命题“若m>0,则方程x2+x-m=0有实根”的逆否命题为“若方程x2+x-m=0无实根,则m≤0”;
④由曲线
| x2 |
| 8-k |
| y2 |
| k+4 |
解答:解:①∵“x=2”⇒“x2-5x+6=0”,
“x2-5x+6=0”⇒“x=2,或x=3”,
∴“x=2”是“x2-5x+6=0”的充分不必要条件,故①是真命题;
②若a>b,c>0,则ac>bc;若a>b,c≤0,则ac≤bc,故②是假命题;
③命题“若m>0,则方程x2+x-m=0有实根”的逆否命题为“若方程x2+x-m=0无实根,则m≤0”,故③是真命题;
④∵曲线
+
=1是椭圆,
∴
,解得-4<k<2,或2<k<8.故④是假命题.
故答案为:①③.
“x2-5x+6=0”⇒“x=2,或x=3”,
∴“x=2”是“x2-5x+6=0”的充分不必要条件,故①是真命题;
②若a>b,c>0,则ac>bc;若a>b,c≤0,则ac≤bc,故②是假命题;
③命题“若m>0,则方程x2+x-m=0有实根”的逆否命题为“若方程x2+x-m=0无实根,则m≤0”,故③是真命题;
④∵曲线
| x2 |
| 8-k |
| y2 |
| k+4 |
∴
|
故答案为:①③.
点评:本题考查命题的真假判断,是基础题.解题时要认真审题,仔细解答.

练习册系列答案
相关题目
 ,对
,对 都有
都有 ,则
,则 为偶函数
为偶函数 ,若对
,若对 ,都有
,都有 ,则函数
,则函数 中心对称
中心对称 与
与 是奇函数
是奇函数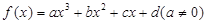 的图形一定是对称中心在图像上的中心对称图形。
的图形一定是对称中心在图像上的中心对称图形。 有两不同极值点
有两不同极值点 ,若
,若 ,且
,且 ,则关于的方程
,则关于的方程 的不同实根个数必有三个.
的不同实根个数必有三个.