题目内容
已知函数 .
.
(1)求 的最小正周期和最小值;
的最小正周期和最小值;
(2)若不等式 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(1) ,
, ;(2)
;(2) .
.
解析试题分析:(1)由于函数 中含有常数
中含有常数 ,
, ,先求
,先求 ,再令
,再令 ,
, ,分别求出
,分别求出 ,
, ,再利用两个角的和的正弦公式变形为
,再利用两个角的和的正弦公式变形为 ,即可求得最小正正周期与最值;(2)当
,即可求得最小正正周期与最值;(2)当 时,利用(1)的结论求得
时,利用(1)的结论求得 ,
, 时不等式
时不等式 恒成立等价于
恒成立等价于 在
在 时恒成立.
时恒成立.
试题解析:(1)
 ,
,
 ,
,
令 得
得 ,解得
,解得 ,
,
 ,
,
 .
. 最小正周期
最小正周期 ,最小值为
,最小值为 . 6分
. 6分
(2)有(1)知 ,当
,当 时
时 ,
,
 ,则
,则 , 8分
, 8分
又对任意 ,
, 恒成立.
恒成立.
 ,即
,即 . 12分
. 12分
考点:导数的计算,三角函数中两个角的正弦公式,恒成立.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 时,求函数
时,求函数 的极值;
的极值; ,
, 的三个顶点
的三个顶点 在函数
在函数 ,
, 、
、 、
、 分别为
分别为
 =
= ,
, =
= ,若曲线
,若曲线 和曲线
和曲线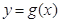 都过点P(0,2),且在点P处有相同的切线
都过点P(0,2),且在点P处有相同的切线 .
. ,
, ,
, ,
, 的值;
的值; 时,
时, ≤
≤ ,求
,求 的取值范围.
的取值范围. +
+ ,g(x)=
,g(x)= ln(2ex)(其中e为自然对数的底数)
ln(2ex)(其中e为自然对数的底数) }中,a1=1,
}中,a1=1,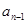 )(n≥2),求证:
)(n≥2),求证: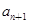 <
< <
< .
. .
. 在
在 上单调递增,求实数
上单调递增,求实数 的取值范围.
的取值范围. ,若
,若 的最小值是
的最小值是 ,求函数
,求函数 和
和 是函数
是函数 的两个极值点,其中
的两个极值点,其中 ,
, .
. 的取值范围;
的取值范围; ,求
,求 的最大值.注:e是自然对数的底.
的最大值.注:e是自然对数的底. ,(
,( 且
且 ).
). ,令
,令 ,试判断函数
,试判断函数 在
在 上的单调性并证明你的结论;
上的单调性并证明你的结论; 且
且
 的定义域和值域都是
的定义域和值域都是 的最大值;
的最大值; 对
对 恒成立,求实数
恒成立,求实数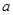 的取值范围;
的取值范围; .
. 的极大值和极小值;
的极大值和极小值; 时,
时, 恒成立,求
恒成立,求 的取值范围.
的取值范围. .
. 时,求曲线
时,求曲线 在
在 处的切线方程;
处的切线方程; 的单调性.
的单调性.