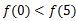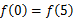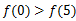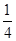题目内容
已知函数f(x)= x3-x2+ax-a(a∈R).
x3-x2+ax-a(a∈R).
(1)当a=-3时,求函数f(x)的极值.
(2)若函数f(x)的图象与x轴有且只有一个交点,求a的取值范围.
 x3-x2+ax-a(a∈R).
x3-x2+ax-a(a∈R).(1)当a=-3时,求函数f(x)的极值.
(2)若函数f(x)的图象与x轴有且只有一个交点,求a的取值范围.
(1) 当x=-1时,函数f(x)取得极大值为f(-1)=- -1+3+3=
-1+3+3=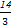 ,
,
当x=3时,函数f(x)取得极小值为f(3)= ×27-9-9+3=-6.
×27-9-9+3=-6.
(2) (0,+∞)
 -1+3+3=
-1+3+3=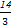 ,
,当x=3时,函数f(x)取得极小值为f(3)=
 ×27-9-9+3=-6.
×27-9-9+3=-6.(2) (0,+∞)
(1)当a=-3时,f(x)= x3-x2-3x+3.
x3-x2-3x+3.
f'(x)=x2-2x-3=(x-3)(x+1).
令f'(x)=0,得x1=-1,x2=3.
当x<-1时,f'(x)>0,
则函数在(-∞,-1)上是增函数,
当-1<x<3时,f'(x)<0,
则函数在(-1,3)上是减函数,
当x>3时,f'(x)>0,
则函数在(3,+∞)上是增函数.
所以当x=-1时,函数f(x)取得极大值为f(-1)=- -1+3+3=
-1+3+3=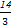 ,
,
当x=3时,函数f(x)取得极小值为f(3)= ×27-9-9+3=-6.
×27-9-9+3=-6.
(2)因为f'(x)=x2-2x+a,
所以Δ=4-4a=4(1-a).
①当a≥1时,则Δ≤0,∴f'(x)≥0在R上恒成立,所以f(x)在R上单调递增.
f(0)=-a<0,f(3)=2a>0,所以,当a≥1时函数的图象与x轴有且只有一个交点.
②a<1时,则Δ>0,∴f'(x)=0有两个不等实数根,不妨设为x1,x2(x1<x2),∴x1+x2=2,x1·x2=a,
则
∵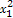 -2x1+a=0,∴a=-
-2x1+a=0,∴a=-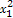 +2x1,
+2x1,
∴f(x1)=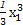 -
-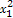 +ax1-a
+ax1-a
=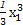 -
-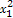 +ax1+
+ax1+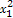 -2x1
-2x1
=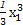 +(a-2)x1
+(a-2)x1
= x1[
x1[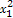 +3(a-2)],
+3(a-2)],
同理f(x2)= x2[
x2[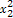 +3(a-2)].
+3(a-2)].
∴f(x1)·f(x2)= x1x2[
x1x2[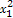 +3(a-2)][
+3(a-2)][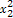 +3(a-2)]=
+3(a-2)]= a(a2-3a+3).
a(a2-3a+3).
令f(x1)·f(x2)>0,解得a>0.
而当0<a<1时,f(0)=-a<0,f(3)=2a>0.
故0<a<1时,函数f(x)的图象与x轴有且只有一个交点.
综上所述,a的取值范围是(0,+∞).
 x3-x2-3x+3.
x3-x2-3x+3.f'(x)=x2-2x-3=(x-3)(x+1).
令f'(x)=0,得x1=-1,x2=3.
当x<-1时,f'(x)>0,
则函数在(-∞,-1)上是增函数,
当-1<x<3时,f'(x)<0,
则函数在(-1,3)上是减函数,
当x>3时,f'(x)>0,
则函数在(3,+∞)上是增函数.
所以当x=-1时,函数f(x)取得极大值为f(-1)=-
 -1+3+3=
-1+3+3=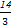 ,
,当x=3时,函数f(x)取得极小值为f(3)=
 ×27-9-9+3=-6.
×27-9-9+3=-6.(2)因为f'(x)=x2-2x+a,
所以Δ=4-4a=4(1-a).
①当a≥1时,则Δ≤0,∴f'(x)≥0在R上恒成立,所以f(x)在R上单调递增.
f(0)=-a<0,f(3)=2a>0,所以,当a≥1时函数的图象与x轴有且只有一个交点.
②a<1时,则Δ>0,∴f'(x)=0有两个不等实数根,不妨设为x1,x2(x1<x2),∴x1+x2=2,x1·x2=a,
则
| x | (-∞,x1) | x1 | (x1,x2) | x2 | (x2,+∞) |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | ↗ | 极大值 | ↘ | 极小值 | ↗ |
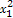 -2x1+a=0,∴a=-
-2x1+a=0,∴a=-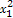 +2x1,
+2x1,∴f(x1)=
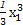 -
-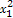 +ax1-a
+ax1-a=
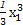 -
-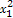 +ax1+
+ax1+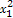 -2x1
-2x1=
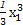 +(a-2)x1
+(a-2)x1=
 x1[
x1[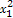 +3(a-2)],
+3(a-2)],同理f(x2)=
 x2[
x2[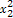 +3(a-2)].
+3(a-2)].∴f(x1)·f(x2)=
 x1x2[
x1x2[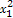 +3(a-2)][
+3(a-2)][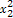 +3(a-2)]=
+3(a-2)]= a(a2-3a+3).
a(a2-3a+3).令f(x1)·f(x2)>0,解得a>0.
而当0<a<1时,f(0)=-a<0,f(3)=2a>0.
故0<a<1时,函数f(x)的图象与x轴有且只有一个交点.
综上所述,a的取值范围是(0,+∞).

练习册系列答案
相关题目
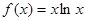 ,
,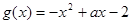 (
(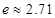 ,
,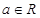 ).
).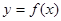 在点(1,
在点(1,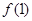 )处的切线与曲线
)处的切线与曲线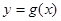 的公共点个数;
的公共点个数;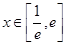 时,若函数
时,若函数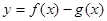 有两个零点,求
有两个零点,求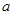 的取值范围.
的取值范围.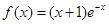 (e为自然对数的底数)
(e为自然对数的底数)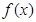 的单调区间;
的单调区间;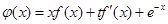 ,存在实数
,存在实数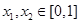 ,使得
,使得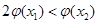 成立,求实数
成立,求实数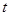 的取值范围
的取值范围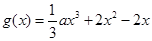 ,函数
,函数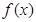 是函数
是函数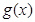 的导函数.
的导函数.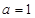 ,求
,求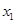 ,
,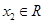 且
且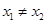 ,都有
,都有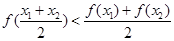 ,求实数
,求实数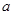 的取值范围;
的取值范围;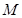 ,使得对任意
,使得对任意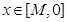 时
时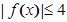 恒成立,求
恒成立,求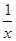 -1.
-1.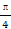 ,则4x与3sin2x的大小关系是( )
,则4x与3sin2x的大小关系是( ) x+3垂直,求切点坐标与切线的方程.
x+3垂直,求切点坐标与切线的方程.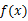 在R上可导,且
在R上可导,且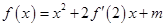 ,则( )
,则( )