题目内容
1.已知三棱锥P-ABC的所有棱长都相等,现沿PA,PB,PC三条侧棱剪开,将其表面展开成一个平面图形,若这个平面图形外接圆的半径为2$\sqrt{6}$,则三棱锥P-ABC的内切球的表面积为3π.分析 根据平面图形外接圆的半径求出三棱锥的棱长,再根据棱长求出高,设内切球的球心为O',半径为r,连接三棱锥的四个顶点得到四个小三棱锥的体积相等,然后根据等积法计算得到半径r,再由球的表面积公式计算即可得到.
解答 解:根据题意几何体为正三棱锥,如图,设棱长为a,
PD=$\frac{\sqrt{3}}{2}$a,OD=$\frac{\sqrt{3}}{6}$a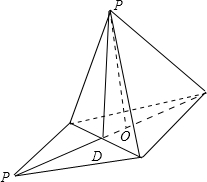 ,OP=$\sqrt{P{D}^{2}-O{D}^{2}}$=$\frac{\sqrt{6}}{3}$a.
,OP=$\sqrt{P{D}^{2}-O{D}^{2}}$=$\frac{\sqrt{6}}{3}$a.
则OD+PD=$\frac{\sqrt{3}}{6}$a+$\frac{\sqrt{3}}{2}$a=$\frac{2\sqrt{3}}{3}$a=2$\sqrt{6}$⇒a=3$\sqrt{2}$,
V棱锥=$\frac{1}{3}$×$\frac{\sqrt{3}}{4}$a2×$\frac{\sqrt{6}}{3}$a=9,
设内切球的球心为O',半径为r,
连接三棱锥的四个顶点得到四个小三棱锥的体积相等,
即为4×$\frac{1}{3}$×$\frac{\sqrt{3}}{4}$a2r=$\frac{\sqrt{3}}{3}$×18r=6$\sqrt{3}$r.
由等积法,可得,9=6$\sqrt{3}$r,
解得,r=$\frac{\sqrt{3}}{2}$.
则内切球的表面积为S=4πr2=3π.
故答案为:3π.
点评 本题主要考查球的表面积的求法,考查等积法的运用,考查三棱锥的体积公式的运用,考查运算能力,属于中档题.

练习册系列答案
相关题目
10.双曲线两条渐近线的夹角为60°,该双曲线的离心率为( )
| A. | $\frac{2}{3}\sqrt{3}$或2 | B. | $\frac{2}{3}\sqrt{3}$或$\sqrt{2}$ | C. | $\sqrt{3}$或2 | D. | $\sqrt{3}$或$\sqrt{2}$ |
 三棱锥S-ABC中,∠SAB=∠SAC=∠ACB=90°,AC=2,BC=$\sqrt{13}$,SB=$\sqrt{29}$,
三棱锥S-ABC中,∠SAB=∠SAC=∠ACB=90°,AC=2,BC=$\sqrt{13}$,SB=$\sqrt{29}$, 如图所示,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.
如图所示,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.